Układ równań z parametrem metodą Gaussa (VIDEO)
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
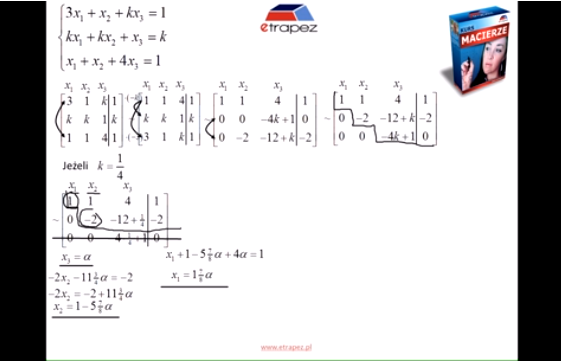
Na filmiku niżej pokazuję, jak rozwiązać układ równań liniowych z parametrem metodą Gaussa. Na studiach często tutaj preferuje się twierdzenie Kroneckera-Capellego, lub bezpośrednio wzory Cramera, ale myślę, że Gauss ma swoje zalety, zobaczcie sami:
Jeśli chcesz się nauczyć metody Gaussa, polecam Ci mocno mój Kurs Macierzy .
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
Nigdzie, ale to nigdzie nie mogę znaleźć odpowiedzi na moje pytanie, a niestety muszę znać odpowiedz. Jeżeli jest układ liniowy i są już zrobione schodki i na jednym z nich są 2 wartości to muszę zastosować parametr – to wiem. Ale w jakim przypadku nie mogłabym użyć któregoś z nich? Cały czas byłam przekonana, że nie ma różnicy która z wartości wezmę jako parametr. Pomocy! ?
Gdybym teraz chciał wyznaczyć to rozwiązanie dla p-3 to liczę tak samo wyznacznik macierzy i wyznaczniki dla zmiennych, tyle że bez podstawiania za p i q?
Witam serdecznie,
Spotkałam się na egzaminie z matematyki z poniższym zadaniem:
Dla jakich wartości p i q układ równań liniowych:
3x-2y+z=q
5x-8y+9z=3
2x+y+pz=1
ma:
1. jedno i tylko jedno rozwiązanie
2. nieskończenie wiele rozwiązań
3. nie ma rozwiązania
Po egzaminie otrzymałam informację, że zadanie powinno być rozwiązane metodą Kroneckera (co wzbudziło moje wątpliwości, gdyż dla mnie układ ma więcej niewiadomych niż równań). Wiem że wartość p=-3, a wartość q=-5/3 jednakże nie wiem jak do tego dojść. Czy mogę prosić o podpowiedź? niestety do piątku muszę się przygotować do egzaminu poprawkowego, a nigdzie nie mogę znaleźć odpowiedzi. Wolfram określił wartości, aczkolwiek nie rozumiem w jaki sposób zostały one uzyskane. Będę wdzięczna za odpowiedź :). Pozdrawiam, Natalia
poprawka – chodziło o metodę cramera
Witam. Przepraszam, że nie odpowiedziałem, ale pozwolę sobie rozwiązać to zadanie, może komuś się przyda.
Układ ma tylko trzy niewiadome: x,y i z. Zmienne p i q to nie są niewiadome, to są parametry, które trzeba wyznaczyć. Jak najbardziej można więc stosować wzory Cramera.
Zasady są takie:
1. Układ ma jedno i dokładnie jedno rozwiązanie, gdy wyznacznik główny jest różny od zera.
2. Układ ma nieskończenie wiele rozwiązań, gdy wyznacznik główny jest równy zero i wszystkie wyznaczniki przy zmiennych są równe zero.
3. Układ nie ma rozwiązań, gdy wyznacznik główny jest równy zero i chociaż jeden wyznacznik przy zmiennych jest różny od zera.
W=\left| \begin{matrix}
3 & -2 & 1 \\
5 & -8 & 9 \\
2 & 1 & p \end{matrix} \right|=-24p+5-36+16-27+10p=-14p-42
-14p-42=0
-14p=42\quad /:\left( -3 \right)
p=-3
W=0 dla p=-3 i W0 dla r-3. Zatem: układ ma jedno i tylko jedno rozwiązanie dla p-3 i wszystko jedno dla jakiego q.
Dla p=-3:
{{W}_{x}}=\left| \begin{matrix}
q & -2 & 1 \\
3 & -8 & 9 \\
1 & 1 & -3 \end{matrix} \right|=24q+3-18+8-9q-18=15q-25
15q-25=0
15q=25\quad /:15
q=\frac{5}{3}
Czyli dla q\ne \frac{5}{3}i p=-3 układ nie ma rozwiązania.
Liczę dalej dla p=-3 i q=5/3:
{{W}_{y}}=\left| \begin{matrix}
3 & \frac{5}{3} & 1 \\
5 & 3 & 9 \\
2 & 1 & -3 \end{matrix} \right|=-27+5+30-6-27+25=0
{{W}_{z}}=\left| \begin{matrix}
3 & -2 & \frac{5}{3} \\
5 & -8 & 3 \\
2 & 1 & 1 \end{matrix} \right|=-24+\frac{25}{3}-12+\frac{80}{3}-9+10=0
Zatem, mogę pisać odpowiedź:
1. Układ ma jedno i tylko jedno rozwiązanie dla p-3
2. Układ ma nieskończenie wiele rozwiązań dla p=-3 i q=5/3.
3. Układ nie ma rozwiązania dla p=-3 i q5/3.
bardzo dziękuję za odpowiedź :). Życzę sukcesów. Natalia
4×1 + 7×2 -3×3 = 12×1 + (m-1)x2 +3×3 = 5-x1 + 2×2 – 4×3 = -3dla jakiej wartości m układ równań liniowych jest nieoznaczony a dla jakiej sprzeczny bardzo proszę o pomoc!!
tu lepiej widać ten układ 🙁
Panie Krystianie!
Wielkie dzieki!
Jestes niesamowity gość, fenomen na skale miedzynarodową! wszyscy z Krakowa pozdrawiają! 🙂
Pozdrawiam Kraków 🙂