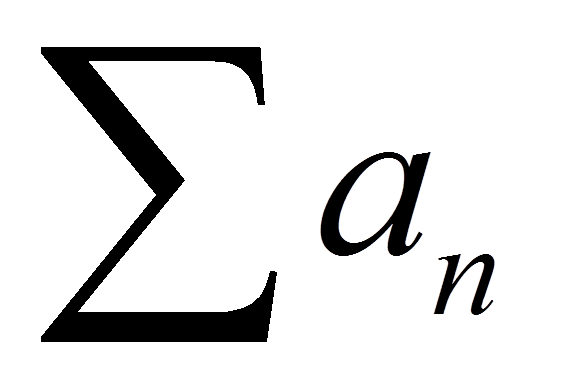
5 Kryteriów Zbieżności Szeregów

---

Jest sobie szereg \sum{{{a}_{n}}} o wyrazach nieujemnych. Mamy sprawdzić, czy jest on zbieżny. Mamy do dyspozycji albo definicję (katorga), albo kryteria (spacer po łące).

Skupmy się na kryteriach.

W moim Kursie Szeregów pokazałem najczęściej używane:

• d’Alemberta
• Cauchy’ego
• porównawcze
• całkowe

Oczywiście nie oznacza to, że lista możliwych kryteriów zbieżności została w ten sposób wyczerpana. W tym poście zajmę się pozostałymi, wprowadzanymi w podręcznikach i przez niektórych profesorów.

Są takie przykłady, w których TYLKO zastosowanie jakiegoś wymyślnego kryterium pozwoli Ci określić zbieżność. Są profesorzy na studiach, którzy dają na egzaminach takie przykłady.

Przerobię:

1. Kryterium “ilorazowe” (z nazewnictwem jest trochę różnie, o czym później)
2. Kryterium “porównawcze ilorazowe”
3. Kryterium Raabego
4. Kryterium Bertranda
5. Kryterium Jermakowa

Zaczynam:

1. Kryterium ilorazowe

Jeżeli mamy dwa szeregi \sum{{{a}_{n}}} i \sum{{{b}_{n}}} , oraz istnieje granica:

\underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}_{n}}}{{{b}_{n}}}

wtedy jeżeli:

• 0<\underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}_{n}}}{{{b}_{n}}}<\infty oba szeregi są równocześnie albo zbieżne, albo rozbieżne
• \underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}_{n}}}{{{b}_{n}}}=0 ze zbieżności szeregu \sum{{{b}_{n}}} wynika zbieżność szeregu \sum{{{a}_{n}}}
• \underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}_{n}}}{{{b}_{n}}}=\infty z rozbieżności szeregu \sum{{{b}_{n}}} wynika rozbieżność szeregu \sum{{{a}_{n}}}

W praktyce robota z kryterium wygląda tak, że mam na wejściu jakiś szereg \sum{{{a}_{n}}} i muszę sam wykombinować taki szereg \sum{{{b}_{n}}} , o znanej już z góry zbieżności (lub rozbieżności), żeby granica \underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}_{n}}}{{{b}_{n}}} określiła mi zbieżność/rozbieżność szeregu \sum{{{a}_{n}}} .

Przykład 1

Zbadaj zbieżność szeregu \sum\limits_{n=1}^{\infty }{\left( \ln \left( n+1 \right)-\ln n \right)}

Wyraz \left( \ln \left( n+1 \right)-\ln n \right) podzielę przez \frac{1}{n} . O szeregu \sum\limits_{n=1}^{\infty }{\frac{1}{n}} wiem już, że jest to szereg rozbieżny (jest to szereg harmoniczny).

\underset{n\to \infty }{\mathop{\lim }}\,\frac{\ln \left( n+1 \right)-\ln n}{\frac{1}{n}}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{\ln \frac{n+1}{n}}{\frac{1}{n}}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{\ln \left( \tfrac{n}{n}+\tfrac{1}{n} \right)}{\frac{1}{n}}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{\ln \left( 1+\tfrac{1}{n} \right)}{\frac{1}{n}}

A to już wprost ze wzoru \underset{x\to 0}{\mathop{\lim }}\,\frac{\ln \left( 1+x \right)}{x}=1 :

\underset{n\to \infty }{\mathop{\lim }}\,\frac{\ln \left( 1+\tfrac{1}{n} \right)}{\frac{1}{n}}=1

Moja granica \underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}_{n}}}{{{b}_{n}}} z kryterium ilorazowego wyszła równa 1. Zgodnie z kryterium ilorazowym zatem szereg \sum\limits_{n=1}^{\infty }{\left( \ln \left( n+1 \right)-\ln n \right)} jest szeregiem rozbieżnym, ponieważ:

1. \sum\limits_{n=1}^{\infty }{\frac{1}{n}} jest rozbieżny
2. Granica \underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}_{n}}}{{{b}_{n}}}=1 , czyli oba szeregi są albo równocześnie zbieżne, albo równocześnie rozbieżne
3. Czyli muszą być oba równocześnie rozbieżne

Przykład 2

Zbadaj zbieżność szeregu \sum\limits_{n=1}^{\infty }{\frac{1}{{{n}^{2}}-n}} .

Wyraz \frac{1}{{{n}^{2}}-n} podzielę przez \frac{1}{{{n}^{2}}} . O szeregu \sum\limits_{n=1}^{\infty }{\frac{1}{{{n}^{2}}}} wiem już z góry, że jest to szereg zbieżny (szereg Dirichleta – tłumaczę to w swoim Kursie ).

Mam:

\underset{n\to \infty }{\mathop{\lim }}\,\frac{\frac{1}{{{n}^{2}}-n}}{\frac{1}{{{n}^{2}}}}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{1}{{{n}^{2}}-n}\frac{{{n}^{2}}}{1}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{{{n}^{2}}}{{{n}^{2}}-n}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{{{n}^{2}}}{{{n}^{2}}\left( 1-\tfrac{1}{n} \right)}=1

Zatem na mocy kryterium porównawczego szereg \sum\limits_{n=1}^{\infty }{\frac{1}{{{n}^{2}}-n}} jest zbieżny.

Jest tak, dlatego, że:

1. \sum\limits_{n=1}^{\infty }{\frac{1}{{{n}^{2}}}}  jest zbieżny
2. Granica \underset{n\to \infty }{\mathop{\lim }}\,\frac{{{a}_{n}}}{{{b}_{n}}}=1 , czyli oba szeregi są albo równocześnie zbieżne, albo równocześnie rozbieżne
3. Czyli muszą być oba równocześnie zbieżne

2. Kryterium “porównawcze ilorazowe”

Tak je nazwałem, chociaż często przez “porównawcze ilorazowe” rozumie się te kryterium oczko wyżej, czyli moje “ilorazowe”. Nie o nazwy jednak chodzi, tylko o to, że:

Mamy dwa szeregi \sum{{{a}_{n}}} i \sum{{{b}_{n}}} . Jeżeli od pewnego n jest spełniona nierówność:

\frac{{{a}_{n+1}}}{{{a}_{n}}}\le \frac{{{b}_{n+1}}}{{{b}_{n}}}

wtedy:

• ze zbieżności szeregu \sum{{{b}_{n}}} wynika zbieżność szeregu \sum{{{a}_{n}}}
• z rozbieżności szeregu \sum{{{a}_{n}}} wynika rozbieżność szeregu \sum{{{b}_{n}}}

3. Kryterium Raabego

Jest to mocne kryterium, a przynajmniej silniejsze od kryterium d’Alemberta. Oznacza to, że w niektórych przypadkach, gdy kryterium d’Alemberta nie roztrzyga o zbieżności szeregu, kryterium Raabego może to roztrzygnąć.

Mamy szereg \sum{{{a}_{n}}} . Liczymy granicę:

\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)

Jeżeli:

• \underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)>1 wtedy szereg jest zbieżny
• \underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)<1 wtedy szereg jest rozbieżny
• \underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)=1 wtedy nie możemy roztrzygnąć zbieżności szeregu

Przykład 3

Zbadaj zbieżność szeregu \sum\limits_{n=1}^{\infty }{\frac{\left( 2n-1 \right)!!}{\left( 2n \right)!!}\frac{1}{2n+1}}

Ten dziwny znaczek: \left( 2n \right)!! oznacza taką specjalną silnię, w której mnożymy przez wyrazy o 2 mniejsze (a nie o jeden), na przykład: 10!!=10\cdot 8\cdot 6\cdot 4\cdot 2 .

Licząc ten szereg kryterium d’Alemberta otrzymał bym:

\underset{n\to \infty }{\mathop{\lim }}\,\frac{\frac{\left( 2n+1 \right)!!}{\left( 2n+2 \right)!!}\frac{1}{2n+3}}{\frac{\left( 2n-1 \right)!!}{\left( 2n \right)!!}\frac{1}{2n+1}}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{\left( 2n+1 \right)\left( 2n-1 \right)\left( 2n-3 \right)\cdot \ldots \cdot 1}{\left( 2n+2 \right)\left( 2n \right)\left( 2n-2 \right)\cdot \ldots \cdot 2}\frac{1}{2n+3}\frac{\left( 2n \right)\left( 2n-2 \right)\cdot \ldots \cdot 2}{\left( 2n-1 \right)\left( 2n-3 \right)\cdot \ldots \cdot 1}\frac{2n+1}{1}= =\underset{n\to \infty }{\mathop{\lim }}\,\frac{2n+1}{2n+2}\frac{2n+1}{2n+3}=1

Czyli kryterium d’Alemberta jest tu bezradne.

Liczę granicę z kryterium Raabego:

\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{\frac{\left( 2n-1 \right)!!}{\left( 2n \right)!!}\frac{1}{2n+1}}{\frac{\left( 2n+1 \right)!!}{\left( 2n+2 \right)!!}\frac{1}{2n+3}}-1 \right)=\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{\left( 2n-1 \right)\left( 2n-3 \right)\cdot \ldots \cdot 1}{\left( 2n \right)\left( 2n-2 \right)\cdot \ldots \cdot 2}\frac{1}{2n+1}\frac{\left( 2n+2 \right)\left( 2n \right)\left( 2n-2 \right)\cdot \ldots \cdot 2}{\left( 2n+1 \right)\left( 2n-1 \right)\left( 2n-3 \right)\cdot \ldots \cdot 1}\frac{2n+3}{1}-1 \right)= =\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{\left( 2n+2 \right)\left( 2n+3 \right)}{{{\left( 2n+1 \right)}^{2}}}-1 \right)=\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{4{{n}^{2}}+10n+6}{{{\left( 2n+1 \right)}^{2}}}-\frac{{{\left( 2n+1 \right)}^{2}}}{{{\left( 2n+1 \right)}^{2}}} \right)=\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{4{{n}^{2}}+10n+6-\left( 4{{n}^{2}}+4n+1 \right)}{{{\left( 2n+1 \right)}^{2}}} \right)=\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{6n+5}{{{\left( 2n+1 \right)}^{2}}} \right)= =\underset{n\to \infty }{\mathop{\lim }}\,\frac{6{{n}^{2}}+5n}{{{\left( 2n+1 \right)}^{2}}}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{{{n}^{2}}\left( 6+\tfrac{5}{n} \right)}{{{n}^{2}}{{\left( 2+\tfrac{1}{n} \right)}^{2}}}=\frac{6}{4}=\frac{3}{2}

Zatem na mocy kryterium Raabego szereg \sum\limits_{n=1}^{\infty }{\frac{\left( 2n-1 \right)!!}{\left( 2n \right)!!}\frac{1}{2n+1}} jest zbieżny, bo granica \underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)>1 .

Przykład 4

Zbadaj zbieżność szeregu \sum\limits_{n=1}^{\infty }{\frac{n!}{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)}}

D’Alembert znowu jest tutaj żałośnie bezradny:

\underset{n\to \infty }{\mathop{\lim }}\,\frac{\frac{\left( n+1 \right)!}{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)\left( n+1\tfrac{1}{2} \right)}}{\frac{n!}{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)}}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{\left( n+1 \right)n!}{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)\left( n+1\tfrac{1}{2} \right)}\frac{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)}{n!}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{n+1}{n+1\tfrac{1}{2}}=1

A kryterium Raabego daje radę:

\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{\frac{n!}{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)}}{\frac{\left( n+1 \right)!}{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)\left( n+1\tfrac{1}{2} \right)}}-1 \right)=\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{n!}{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)}\frac{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)\left( n+1\tfrac{1}{2} \right)}{\left( n+1 \right)n!}-1 \right)= =\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{n+1\tfrac{1}{2}}{n+1}-1 \right)=\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{n+1\tfrac{1}{2}}{n+1}-\frac{n+1}{n+1} \right)=\underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{\tfrac{1}{2}}{n+1} \right)=\underset{n\to \infty }{\mathop{\lim }}\,\frac{\tfrac{1}{2}n}{n+1}=\underset{n\to \infty }{\mathop{\lim }}\,\frac{\tfrac{1}{2}n}{n\left( 1+\tfrac{1}{n} \right)}=\frac{1}{2}

Czyli na mocy kryterium Raabego szereg \sum\limits_{n=1}^{\infty }{\frac{n!}{1\tfrac{1}{2}\cdot 2\tfrac{1}{2}\cdot 3\tfrac{1}{2}\cdot \ldots \cdot \left( n+\tfrac{1}{2} \right)}} jest rozbieżny, bo granica \underset{n\to \infty }{\mathop{\lim }}\,n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)<1 .

4. Kryterium Bertranda

Jest to kryterium jeszcze silniejsze od kryterium Raabego (zadziała w niektórych przypadkach, w których zawiedzie Raabe).

Mamy szereg \sum{{{a}_{n}}} . Liczymy granicę:

\underset{n\to \infty }{\mathop{\lim }}\,\ln n\left[ n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)-1 \right]

Jeżeli:

• \underset{n\to \infty }{\mathop{\lim }}\,\ln n\left[ n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)-1 \right]>1  wtedy szereg jest zbieżny
• \underset{n\to \infty }{\mathop{\lim }}\,\ln n\left[ n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)-1 \right]<1  wtedy szereg jest rozbieżny
• \underset{n\to \infty }{\mathop{\lim }}\,\ln n\left[ n\left( \frac{{{a}_{n}}}{{{a}_{n+1}}}-1 \right)-1 \right]=1  wtedy nie możemy roztrzygnąć zbieżności szeregu

Jak widać, kryterium Bertranda jest silniejsze od Raabego, ale kosztem tego, że liczyć trzeba bardziej skomplikowaną granicę (tak samo jak Raabego było silniejsze od d’Alemberta kosztem skomplikowania granicy).

5. Kryterium Jermakowa

Kryterium wykorzystuje funkcje (podobnie) jak kryterium całkowe (omawiam je w moim Kursie). Nie potrzeba jednak do niego żadnych całek. Załóżmy, że mamy funkcję f\left( x \right) , utworzoną z ciągu {{a}_{n}} w szeregu \sum{{{a}_{n}}} ( {{a}_{n}}=f\left( n \right) ), nieujemną i malejącą – wszystko tak jak w kryterium całkowym. Wówczas…

Kryterium Jermakowa

Badamy funkcję:

\frac{f\left( {{e}^{x}} \right){{e}^{x}}}{f\left( x \right)}

Jeżeli od pewnego x>{{x}_{0}}

• \frac{f\left( {{e}^{x}} \right){{e}^{x}}}{f\left( x \right)}\le q<1 wtedy szereg jest zbieżny (funkcja musi być ograniczona od góry ułamkiem właściwym)
• \frac{f\left( {{e}^{x}} \right){{e}^{x}}}{f\left( x \right)}\ge 1 wtedy szereg jest rozbieżny (funkcja musi być ograniczona od dołu liczbą 1)

Przykład 5

Zbadaj zbieżność szeregu \sum\limits_{n=2}^{\infty }{\frac{1}{n{{\ln }^{2}}n}}

Szereg można zrobić kryterium całkowym. Szybciej będzie jednak machnąć “Jermakowem”. Funkcja \frac{1}{x{{\ln }^{2}}x} spełnia założenia, bo ma wyrazy nieujemne dla x>2 i jest malejąc w tym przedziale.

Czyli tworzymy do niej funkcję z twierdzenia Jermakowa:

\frac{f\left( {{e}^{x}} \right){{e}^{x}}}{f\left( x \right)}=\frac{\tfrac{1}{{{e}^{x}}{{\ln }^{2}}{{e}^{x}}}{{e}^{x}}}{\tfrac{1}{x{{\ln }^{2}}x}}=\frac{\tfrac{1}{{{\left( \ln {{e}^{x}} \right)}^{2}}}}{\tfrac{1}{x{{\ln }^{2}}x}}=\frac{1}{{{\left( x\ln e \right)}^{2}}}\frac{x{{\ln }^{2}}x}{1}=\frac{1}{{{x}^{2}}}\frac{x{{\ln }^{2}}x}{1}=\frac{{{\ln }^{2}}x}{x}

Wraz ze wzrostem x to wyrażenie dąży do 0 :

\underset{x\to \infty }{\mathop{\lim }}\,\frac{{{\ln }^{2}}x}{x}\underset{H}{\mathop{=}}\,\underset{x\to \infty }{\mathop{\lim }}\,\frac{{{\left( {{\ln }^{2}}x \right)}^{\prime }}}{{{\left( x \right)}^{\prime }}}=\underset{x\to \infty }{\mathop{\lim }}\,\frac{2\ln x\cdot \tfrac{1}{x}}{1}=\underset{x\to \infty }{\mathop{\lim }}\,\frac{2\ln x}{x}\underset{H}{\mathop{=}}\,\underset{x\to \infty }{\mathop{\lim }}\,\frac{{{\left( 2\ln x \right)}^{\prime }}}{{{\left( x \right)}^{\prime }}}=\underset{x\to \infty }{\mathop{\lim }}\,\frac{2}{x}=0

Zatem z pewnością jest ograniczone od góry jakimś ułamkiem właściwym q , o którym mowa w twierdzeniu.

Zatem na mocy twierdzenia Jermakowa jest to szereg zbieżny.

Podsumowanie

Dodatkowych kryteriów zbieżności z tego postu nie traktuj jako kryteria alternatywne, do tych bardziej znanych, ale jak zawodników rezerwowych, którzy wchodzą do gry, kiedy podstawowy team zawodzi.

Są one przeważnie bardziej skomplikowane od swoich popularnych “zamienników” i wymagają użycia cięższej artylerii. Ale w matematyce i miłości wszystkie chwyty dozwolone 🙂