Funktionsgrenzenrechner (VERALTET) + Neuer Rechner

Ankündigung

Leider musste ich nach über 12 Jahren, in denen ich einen kostenlosen Rechner für Funktionsgrenzen angeboten habe, ihn „abschalten“.

Der Rechner war ein einfaches „Widget“ der Seite WolframAlpha. Vor einiger Zeit hat WolframAlpha seine Politik bezüglich Widgets geändert. Beispielsweise berechnen sie nicht mehr „vor Ort“, sondern leiten den Benutzer zur Seite WolframAlpha weiter.

Ich entschuldige mich bei allen bisherigen Benutzern des Funktionsgrenzen-Rechners für die Unannehmlichkeiten.

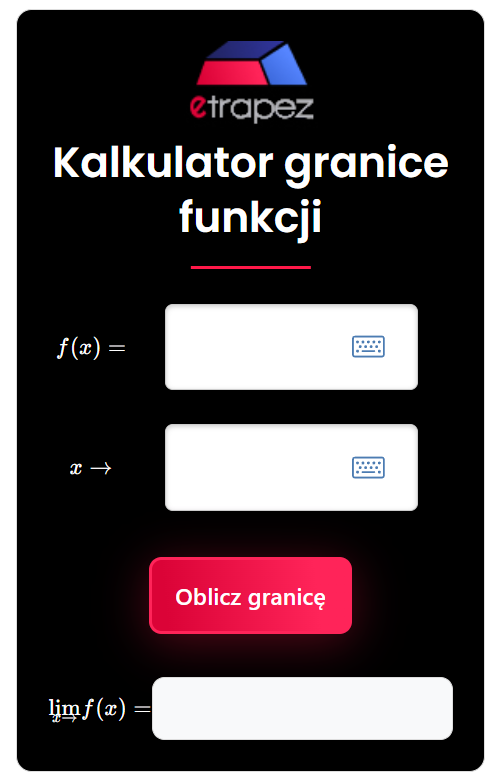
Neuer Funktionsgrenzen-Rechner

Ich lade Sie auch zum neuen Funktionsgrenzen-Rechner ein, den ich mit Open-Source-Technologie erstellt habe. Zugang zu ihm und anderen interaktiven Tools erhalten Sie mit einem Abonnement für nur 5,99 PLN/Monat (oder günstiger in Mehrmonatsoptionen) auf der Website:

Interaktywne Zadanie Domowe

Und der Rechner selbst sieht so aus:

Viele Grüße und viel Erfolg!

Krystian Karczyński

Krystian Karczyński

Założyciel i szef serwisu eTrapez.

Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.

Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.

Related Posts

Verbotene Formeln für unbestimmte Integrale – Ableitung der Formeln

Posted on 8 August 2024

Homogene Gleichungssysteme (Anzahl der Lösungen unter Verwendung der Matrixrang)

Posted on 21 Juni 2024

Eigenwerte und Eigenvektoren einer Matrix

Posted on 9 Februar 2024