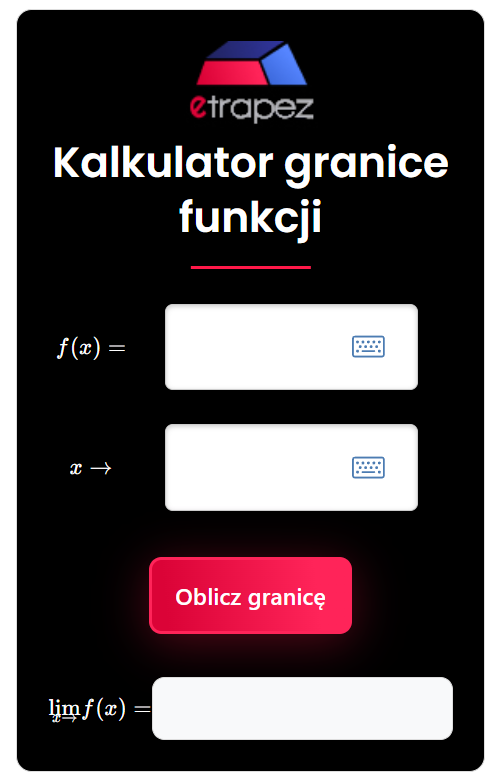
Kalkulator granice funkcji (NIEAKTUALNE) + nowy kalkulator
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Ogłoszenie
Niestety, po ponad 12 latach od udostępnienia przeze mnie darmowego kalkulatora do granic funkcji, musiałem go “wyłączyć”.
Kalkulator był prostym “widgetem” strony WolframAlpha. Jakiś czas temu Wolframalpha zmienił swoją politykę odnośnie widgetów. Między innymi: przestały one obliczać “na miejscu”, tylko przerzucają użytkownika na stronę WolframAlpha .
Przepraszam za kłopot wszystkich dotychczasowych użytkowników Kalkulatora Do Granic Funkcji.
Nowy kalkulator granic funkcji
Zapraszam też do nowego kalkulatora granic funkcji, stworzonego już przeze mnie w technologii Open Source. Dostęp do niego oraz do innych interaktywnych narzędzi możecie uzyskać w ramach subskrypcji za jedyne 5,99 zł / miesiąc (lub taniej w opcjach kilkumiesięcznych) na stronie:
A sam kalkulator wygląda tak:
Pozdrawiam i powodzenia!
Krystian Karczyński
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
Męczę się długo z tym przykładem i nie ma pojęcia jak go zrobić. Dlaczego w: “lim x dąży do nieskończoności: e^x-x^2″=nieskończoność?
f(x)=xarccos(x/(1-x)) x->1-
co oznacza ioo w wyniku granicy
Bardzo proszę o rozwiązanie granicy funkcji: lim x->1 lnx * cos( π/x-1)
Mam problem z jedną granicą, wyszło mi 0 a robiłem ten przykład metodą mnożenia przez sprzężenie, natomiast na kalkulatorze pokazuje że dąży do nieskończoności.
lim x->oo x \sqrt(3) – \sqrt(3n^2+8)
Czy da się wpisać w kalkulator PI/2? Bo samo PI działa, a przez 2 na żaden sposób nie chce obliczyć nie rozumie
Mi PI/2 działa… A jaka jest cała formuła i do czego ma dążyć x?
Witam pomoże ktoś z granicą:lim x->PI/2 (tgx)^1/(x-PI/2) ?
Czy ktoś pomoże z taką granicą: lim x->oo (((sinx)^2)*lnx)/(x^1/3)
A jak obliczyć granice lim x->0+ 2x*ln(arcsinx)
Dobry Wieczór. Przygotowuje się do kolokwium i chciałbym policzyć jedną granicę, a na kalkulatorze wychodzi jakiś dziwny wynik. Raz zero, raz nieskończoność. Przykład:lim przy x -> nieskończoność (3n+7/3n-2)^-4n
Witam! Potrzebuję pomocy : lim x->o x^x
Dzień dobry! Pilnie potrzebuję pomocy z jednym przykładem. Liczę i liczę, a doliczyć się nie mogę.Z gory dziękuję za pomoc 🙂 lim x->oo (x-lnx)
https://www.youtube.com/watch?v=wg4hVSerxPQ
Witam! Potrzebuję natychmiastowej pomocy z jednym przykładem. Męczę się strasznie, lecz nie mogę go zrobić. Moja profesorka jest straszna. Z góry dziękuję za pomoc.
Granica ta tylko na pierwszy rzut oka wydaje się straszna 🙂
Wystarczy zauważyć taki myk, że występują tutaj po prostu liczby do potęgi “x”. Liczbę e jak i
można potraktować na równi jakby stała tam 
czy 
. W takich sytuacjach postępuje typowo, czyli wyciągam przed nawias największe potęgi z licznika i mianownika, pamiętając, że 
oraz 
Teraz
więc w granicy da 
. Pozostałe wyrażenia podniesione do potęgi x dążą do 
stąd ostateczna granica:
Witam serdecznie mam problem z taka granica lim x →∞ ((x-3)e^(x/(3-x))-x/e) ma wyjsc -6/e mi jakos wychodzi -3/e i nie wiem co zrobic 🙁
jak obliczyć granicę lim_(x->-oo) (sqrt(1+x^2)+x)
Granicę liczymy standardowo mnożąc przez sprzężenie, trzeba tylko uważać, że mamy do czynienia z
. Wygląda to następująco:
Dobry wieczór, chcąc policzyć granicę z f(x)=\sqrt(x(x+1))-x dążącą do nieskończoności kalkulator pokazuje mi wynik 1/2, z moich obliczeń wynika że jest to 2, proszę o pomoc..
Już znalazłem błąd w moich obliczeniach.
Jak obliczyć taką granicę bez używania pochodnych ?lim_(x->-1) (sqrt(4 x + 5) – x^2)/(x^2 – 1)
W obliczeniach należy wykonać mnożenie przez sprzężenia tzn.
następnie rozkładamy
korzystając ze schematu Hornera dla 
i dostajemy 
.
Dalej
Dzień dobry, Jak obliczyć taką granicę: lim x–> oo ln(lnx)/xlnx Bardzo proszę o pomoc.
Dzień dobry,
Trzeba pociągnąć regułą de l’Hospitala:
Czy mógłby ktoś mi wytłumaczyć dlaczego lim x-> -oo z ln(x) jest równy nieskończoność?
Witam
Logarytm naturalny jest określony tylko dla
. Granice można odczytać z wykresu funkcji 
Na wykresie widać, że jeżeli x dąży do nieskończoności to wykres ucieka do góry czyli
; jeżeli natomiast x dąży do zera od prawej strony to wykres ucieka w dół czyli 
.
Nie ma natomiast granicy w
z uwagi na dziedzinę logarytmu.
Świetne wytłumaczenie, kula jest okrągła – bo koło jest okrągłe. Fajnie się argumentuje w tych ciemnych czasach historii… Pójdźmy dalej… Dlaczego masło smakuje masłem – bo jest maślane. Dziękuję za brawa – jestem tak zajebisty jak autor wpisu powyżej
Dzień Dobry!Chciałbym zapytać w jaki sposób mogę wpisać do kalkulatora wyrażenie cos(2x!)
Pomóżcie proszę! Znalazłam w znanym zbiorze bardzo skomplikowane rozwiązanie granicy. Czy to naprawdę taki trudny przypadek?
Nie, to niezbyt trudny przypadek. Należy skorzystać z reguły de Hospitala:
Na początku sprawdzamy, co do czego zmierza:
Mamy więc symbol nieoznaczony.
Przekształcamy go do symbolu nieoznaczonego, w którym można zastosować regułę de Hospitala (pokazałem jak to się robi w Kursie Granic: https://etrapez.pl/produkt/kurs-granice/ ), stosujemy regułę, wszystko ładnie się upraszcza i mamy wynik:
Bardzo dziękuję za pomoc !!! 🙂
hej
Pójdzie to tak (należy skorzystać z reguły de l’Hospitala):
Dziękuję za pomoc 🙂 P.S. Wkradł się mały błąd, (x^4)’=4x^3
Poprawione. Przepraszamy za ta “literówka”. Dalej już idzie poprawnie 🙂
Proszę pomóżcie:)Jak policzyć z d’H lim przy x dążącym do 0+ dla x*e^1/x. Wiem, że ma wyjść nieskończoność? Znalazłam, w Krysickim uzasadnienie, ale strasznie skomplikowane.
Wystarczy “wrzucić” x do mianownika, a dokładniej:
W granicy wystarczy skorzystać z wartości funkcji sinus tzn.
, dostaniemy
Granica obustronna również wynosi zero.
Mam problem z taką granicą nie mam pojecia jak sie za nia zabrac, proszę o pomoc:
W rozwiązaniu wykorzystamy regułę De l’Hospitala oraz własności logarytmów tzn.
Obliczymy granicę
(wydaję mi się, że granica w 
jest ciążka do policzenia i tym samym granica obustronna w 
; po obliczeniu jeszcze powrócę do tego problemu).
Zaczynamy
Dalej
Powracając do
dostajemy
Granica w
tą metoda nie jest możliwa do policzenia ze względu na dziedzinę logarytmu naturalnego 
. Możemy liczyć tylko granicę prawostronną w zerze. Granica 
nie ma sensu.
Mam problem z tą granicą, powinno wyjść chyba zero a ja nie wiem czemu.
Trzeba tak zadziałać:
(bo
)
Polecam, przy okazji mój:
Kurs Granic, https://etrapez.pl/produkt/kurs-granice/
Obliczy mi ktoś ? męcze się z tym od dwóch dni .. ;( ( 5(n+1)!-2(n-1)!)/(3n!-(n+1)! n->oo oraz lim –>4 (x+x^1/2-6)/(x-(5*x^1/2)-6) liczylam z d’Hospitala i wyszlo mi -5 a tutaj na kalkulatorze wychodzi 0
1.
2.
Najprawdopodobniej błąd w zapisach. Chyba powinno być tak:
Mam obliczyc granice zmierzajaca do zera tgx/x^3 – sinx/x^3. W kalkulatorze wychodzi 1/2 a mi zero . Zrobilam z metody de’l Hospitala poniewaz na poczatku wychodzi indeks [0/0] i dalej z pochodnych . Dlaczego wyniki sie roznia ?
Nie mogę rozwiązać tej granicy ( (x^(x)*2^(x))/(x!) a x dąży do nieskończoności) mam wskazówkę, że 0<(ax+1)/(ax)<1 ale wychodzi mi 2e, więc murze udowodnić innym sposobem.. ale nie mam pojęcia jakim..
Dzień dobry! Mam taki kłopot z granicą . W przypadku gdy funkcja dąży do -oo a wygląda tak: lim =2^x to jakim cudem wychodzi że jest to równe zero? Czy liczba podniesiona do potęgi -oo zawsze będzie zerem? Proszę o pomoc. Serdecznie pozdrawiam. K.
Witam!
Jeśli chodzi o taką granicę, przy x dążącym do
zależy jaką liczbę podnosisz do potęgi, większą od 1 czy ułamek.
Bo ten minus w potędze jaki się pojawi (po podstawieniu granicy) – zamienia podstawę na odwrotną, to znaczy wykorzystuje się zależność potęg
Stąd w takich granicach, jeśli liczba podniesiona do potęgi
jest większa od 1, zamieni się na ułamek podnoszony do potęgi 
, a to zawsze będzie zerem 🙂
Wynik wziął się z wzoru
Witam. Czy byłby mi ktoś w stanie pomóc z takim oto przykładem ? lim x-> -oo ln(x^2+1) / 3-4x^2
Jasne, zapraszam:
Cześć . Ucze się do wrześniowego egzaminu i mam problem z jedym przykładem , za każdym razem wychodzi mi cos innego . Proszę o pomoc jak go rozwiązać po kolei bo coś na pewno robie źle .
(1+3/x)^-x przy x-> oo
Witam, granicę można rozwiązać korzystając ze wzoru
Otrzymamy po drobnym przekształceniu
Lim x->-oo( (2x+1)^4-(2x+3)^4)/((x+3)^3-(3x-1)^3)=
Obliczy ktos? 🙂 ma wyjść 32/13
\underset{{x to \infty }}{\mathop{{lim }}}\frac{{{{{(2x+1)}}^{4}}-{{{(2x+3)}}^{4}}}}{{{{{(x+3)}}^{3}}-{{{(3x-1)}}^{3}}}}
Rozpisuję podane wyrażenia. O ile w mianowniku można by zastosować wzory skróconego mnożenia, poznane jeszcze w szkole w średniej, to w liczniku nie koniecznie znamy/ pamiętamy od razu gotowy wzór.
Wykorzystuje więc wzór ogólny na n-tą potęgę sumy dwóch liczb (do doboru współczynników pomocny jest również tzw. Trójkąt Pascala)
Stąd
\displaystyle {{(a+b)}^{4}}={{a}^{4}}+4{{a}^{3}}b+6{{a}^{2}}{{b}^{2}}+4a{{b}^{3}}+{{b}^{4}}
\displaystyle {{(a+b)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}
\displaystyle {{(a-b)}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}
No to rozpisując mam:
\displaystyle \underset{{x\to \infty }}{\mathop{{lim }}}\frac{{{{{(2x+1)}}^{4}}-{{{(2x+3)}}^{4}}}}{{{{{(x+3)}}^{3}}-{{{(3x-1)}}^{3}}}}=
\displaystyle \underset{{x\to \infty }}{\mathop{{lim }}}\frac{{16{{x}^{4}}+4\cdot 8{{x}^{3}}+6\cdot 4{{x}^{2}}+4\cdot 2x+1-(16{{x}^{4}}+4\cdot 8{{x}^{3}}\cdot 3+6\cdot 4{{x}^{2}}\cdot 9+4\cdot 2x\cdot 27+81)}}{{{{x}^{3}}+3\cdot {{x}^{2}}\cdot 3+3\cdot x\cdot 9+27-(27{{x}^{3}}-3\cdot 9{{x}^{2}}+3\cdot 3x-1)}}
\displaystyle =\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{16{{x}^{4}}+32{{x}^{3}}+24{{x}^{2}}+8x+1-16{{x}^{4}}-96{{x}^{3}}-216{{x}^{2}}-216x-81}}{{{{x}^{3}}+9{{x}^{2}}+27x+27-27{{x}^{3}}+27{{x}^{2}}-9x+1}}=
\displaystyle =\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{-64{{x}^{3}}-192{{x}^{2}}-208x-80}}{{-26{{x}^{3}}+36{{x}^{2}}+18x+28}}=\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{{{x}^{3}}\cdot \left( {-64-\frac{{192}}{x}-\frac{{208}}{{{{x}^{2}}}}-\frac{{80}}{{{{x}^{3}}}}} \right)}}{{{{x}^{3}}\cdot \left( {-26+\frac{{36}}{x}+\frac{{18}}{{{{x}^{2}}}}+\frac{{28}}{{{{x}^{3}}}}} \right)}}=
\displaystyle \underset{{x\to \infty }}{\mathop{{lim }}}\frac{{\left( {-64-\frac{{192}}{x}-\frac{{208}}{{{{x}^{2}}}}-\frac{{80}}{{{{x}^{3}}}}} \right)}}{{\left( {-26+\frac{{36}}{x}+\frac{{18}}{{{{x}^{2}}}}+\frac{{28}}{{{{x}^{3}}}}} \right)}}=\left[ {\frac{{-64-0-0-0}}{{-26+0+0+0}}} \right]=\frac{{32}}{{13}}
Czemu lim x^2/e^x jest równy 0?
Podstawiając wartość \displaystyle \infty za x mam granicę \displaystyle \left[ {\frac{\infty }{\infty }} \right], dlatego też stosuję regułę de l’Hospitala.
\displaystyle \begin{matrix}\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{{{x}^{2}}}}{{{{e}^{x}}}}=\left[ {\frac{\infty }{\infty }} \right]\overset{H}{\mathop{=}}\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{\left( {{{x}^{2}}} \right)’}}{{\left( {{{e}^{x}}} \right)’}}=\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{2x}}{{{{e}^{x}}}}=\left[ {\frac{\infty }{\infty }} \right]\overset{H}{\mathop{=}}\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{\left( {2x} \right)’}}{{\left( {{{e}^{x}}} \right)’}}=\underset{{x\to \infty }}{\mathop{{lim }}}\frac{2}{{{{e}^{x}}}}=\left[ {\frac{2}{\infty }} \right]=0\end{matrix}
Wynik końcowy powstał wprost z zastosowania wzoru na granicę:
\displaystyle \left[ {\frac{A}{{\pm \infty }}} \right]=0
Co z granicą lim x->oo (1+4/n)^(n-1) ?
\displaystyle \underset{{n\to \infty }}{\mathop{{lim }}}{{\left( {1+\frac{4}{n}} \right)}^{{n-1}}}
Wykorzystać chcę tu wzór:
\displaystyle \underset{{n\to \infty }}{\mathop{{lim }}}{{\left( {1+\frac{a}{\square }} \right)}^{\square }}={{e}^{a}}
Dlatego przekształcam:
\displaystyle \underset{{n\to \infty }}{\mathop{{lim }}}{{\left( {1+\frac{4}{n}} \right)}^{{n-1}}}=\underset{{n\to \infty }}{\mathop{{lim }}}{{\left[ {{{{\left( {1+\frac{4}{n}} \right)}}^{n}}} \right]}^{{\frac{{n-1}}{n}}}}
Wyrażenie w nawiasie kwadratowym dąży do \displaystyle {{e}^{4}}.
Na boku rozpisuję granicę potęgi
\displaystyle \underset{{n\to \infty }}{\mathop{{lim }}}\frac{{n-1}}{n}=\underset{{n\to \infty }}{\mathop{{lim }}}\frac{{n\left( {1-\frac{1}{n}} \right)}}{n}=\underset{{n\to \infty }}{\mathop{{lim }}}\left( {1-\frac{1}{n}} \right)=1-0=1
Mam więc ostatecznie:
\displaystyle \underset{{n\to \infty }}{\mathop{{lim }}}{{\left[ {{{{\left( {1+\frac{4}{n}} \right)}}^{n}}} \right]}^{{\frac{{n-1}}{n}}}}={{\left[ {{{e}^{4}}} \right]}^{1}}={{e}^{4}}
wprowadziłam dla sprawdzenia granicę (x^2-9)/(x^2-3x) przy x dążącym do 3 mi wychodzi 0 natomiast tu pojawia się 2, dlaczego?
w tej granicy, jak się tego nie poprzekształca wychodzi na końcu 0/0. Trzeba policzyć pochodne z tych funkcji i dopiero liczyć granicę, czyli 2x/(2x-3).
Rozwiązanie:
Po sprawdzeniu. że mamy wyraz typu
, licznik rozkładamy na mnożniki wg wzoru mnożenia skroconego 
, w mianowniku wynosimy x za nawiasy, potem ułamek skracamy i podstawiamy 
ponownie:
Jak wprowadzić symbol pi?
PI, obie literki z wielkiej.
Przydatna sprawa 🙂 Jednak nie mogę rozwiązać jednej granicy:
(e^(2x)-1)/ln(1+2x). Wiem, że powinno wyjść 1 (mi wychodzi 0), ale nie mam pojęcia skąd. Mógłbyś mi to wytłumaczyć ?
Rozumiem, że chodzi o granicę funkcji dla x dążącego do zera tak? 😉
http://www.wolframalpha.com/input/?i=lim+(e%5E(2x)-1)%2Fln(1%2B2x)
A zatem po podstawieniu w granicy \displaystyle \underset{{x\to 0}}{\mathop{{lim }}}\frac{{{{e}^{{2x}}}-1}}{{ln(1+2x)}} wartości zero za “x” mam:
\displaystyle \left[ {\frac{{{{e}^{0}}-1}}{{ln (1+0)}}=\frac{{1-1}}{{ln 1}}=\frac{0}{0}} \right]
Jest to symbol nieoznaczony, dlatego najlepiej jest tu zastosować regułę de l’Hospitala:
\displaystyle \underset{{x\to 0}}{\mathop{{lim }}}\frac{{{{e}^{{2x}}}-1}}{{ln(1+2x)}}=\left[ {\frac{0}{0}} \right]\overset{H}{\mathop{=}}\underset{{x\to 0}}{\mathop{{lim }}}\frac{{\left( {{{e}^{{2x}}}-1} \right)’}}{{\left( {ln(1+2x)} \right)’}}=\underset{{x\to 0}}{\mathop{{lim }}}\frac{{{{e}^{{2x}}}\cdot 2-0}}{{\frac{1}{{1+2x}}\cdot 2}}=
\displaystyle \underset{{x\to 0}}{\mathop{{lim }}}{{e}^{{2x}}}\cdot (1+2x)=\left[ {{{e}^{{2\cdot 0}}}\cdot (1+2\cdot 0)=1\cdot (1+0)} \right]=1
ok, przepraszam znalazłem 🙂
no dobrze a jak wprowadzić pierwiastek ?
sqrt()
czy można wprowadzić pierwiastek np. 3 stopnia?
Tak, należy wpisać x^1/3 🙂