Równania zespolone wielomianowe sprowadzane do kwadratowych

Krystian Karczyński

Sprowadzanie do równań kwadratowych niektórych równań stopnia 4

Wiele równań wielomianowych 4-tego stopnia da się przekształcić na równania kwadratowe znaną dobrze ze szkoły średniej sztuczką opisaną tutaj:

Sprowadzanie do równania kwadratowego

Działa to oczywiście i jak najbardziej także dla wielomianów w liczbach zespolonych.

Przypominam, chodzi o to, że mając równanie:

{{z}^{4}}+3{{z}^{2}}+2=0

Podstawiamy: ${{z}^{2}}=t$

I wychodzimy na równanie kwadratowe:

{{t}^{2}}+3{t}+2=0

Dalej rozwiązujemy je zwykłą deltą i tak dalej, mamy rozwiązania , pamiętając o tym, że tworzymy z nich dwa następne równania:

lub

Rozwiązujemy je i mamy cztery rozwiązania: .

Sprowadzanie do równań kwadratowych niektórych równań większych stopni

Absolutnie nic nie stoi na przeszkodzie, aby tą metodę rozszerzyć na równania stopni większych niż 4 (jeżeli oczywiście dają się one sprowadzić do kwadratowych przez podstawienie).

A więc mając:

2{{z}^{6}}-5{{z}^{3}}+4=0

Można także zauważyć, że jest ono równoważne:

2{( {z}^{3})^{2}}-5{{z}^{3}}+4=0

I po podstawieniu:

Wychodzimy na kwadratowe:

2{{t}^{2}}-5t+4=0

W równaniu:

{{x}^{10}}-3{{x}^{5}}+1=0

Po podstawieniu:

Mamy:

{{t}^{2}}-3t+1=0

I tak dalej, i tak dalej…

Przykład

Weźmy równanie:

z^6+(1-i)z^3-i=0

Podstawiamy $z^2=t$ i mamy:

t^2+(1-i)t-i=0

Dalej liczymy:

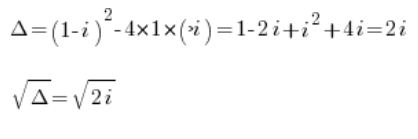
Liczymy te pierwiastki znanymi z liczb zespolonych metodami (pokazanym np. w moim Kursie ).

Mamy lub

Czyli:

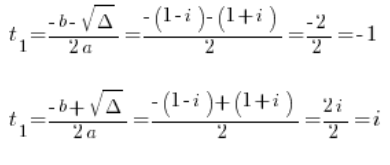
Pamiętamy, że to nie są jeszcze rozwiązania, bo $z^3=t$

Czyli mamy do rozwiązania równania:

z^3=-1

oraz:

z^3=i

Przekształcamy je na:

oraz

i obliczając znowu znanymi metodami mamy trzy pierwiastki z pierwszego równania:

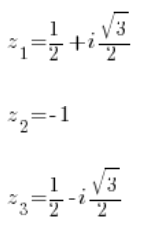
Oraz trzy pierwiastki z drugiego równania:

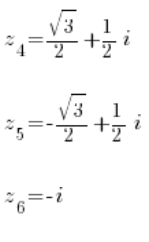
Rozwiązane 🙂

konometria jest dosyć młodą dziedziną wypływającą z ekonomii i matematyki. W praktyce, dzięki modelom ekonometrycznym, możesz „zmierzyć gospodarkę”.Polega to konkretnie na zmierzeniu, jak zachowuje się jedna zmienna w zależności od innych. I na podstawie analizy tego, co było, możesz określać, co będzie się działo w przyszłości.

Wykorzystasz do tego przeróżne obliczenia, testy, schematy. Jedne będą bardzo proste, inne trudniejsze. Jednak najczęściej będzie się liczyło nie to, jak dojdziesz do wyniku, ale jak go zinterpretujesz, odczytasz i jakie wnioski wyciągniesz.

Poniższe Wykłady dotykają najważniejszych pojęć teoretycznych. Jestem przekonana, że pomogę Ci odkrywaniu tego, czym jest ekonometria. I przy okazji uda Ci się zaliczyć ten przedmiot na studiach.

2 Komentarzy

Sebastian
13 lutego 2012 at 12:03

Serdecznie witam, czy może w jakimś kursie jest opisane Twierdzenie Taylora, tzn zadania typu : oszacować dokładość wzoru przyblizonego ??

Odpowiedz
1. Krystian Karczyński
  13 lutego 2012 at 21:12
  
  Witam, tak takie rzeczy są w Kursie Szeregów na Lekcji 9.