W trudniejszych zadaniach na całki oznaczone często warto zachować czujność – zadanie pozornie bardzo ciężkie można rozwiązać prostym wzorem z gimnazjum.
Zadanie na objętość bryły obrotowej
Powiedzmy, że mamy policzyć objętość bryły powstałej przez obrót krzywej:
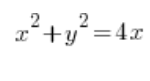
kręcącej się (no O.K., niech będzie „obracającej się”) dookoła osi OX. Kilka ruchów porządkujących znanych ze szkoły średniej…
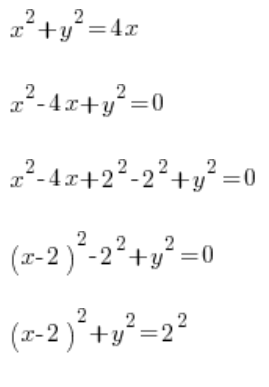
…i orientujemy się, że nasza krzywa to po prostu kółeczko o środku w punkcie (2,0) i promieniu 2. Co teraz? Wyprowadzamy ze wzoru y i forsujemy całką oznaczoną: 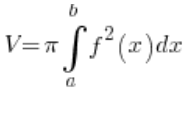 ?
?
Rozwiązanie
Nie… Zatrzymajmy się na chwilę. Wciągnijmy powietrze. Zastanówmy się. Kółeczko… Obraca się… Co nam powstanie w wyniku takiego obrotu? Oczywiście kula. Wzór objętość kuli znamy z gimnazjum:
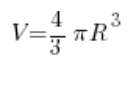
Promień już znamy (równy jest dwa), czyli:
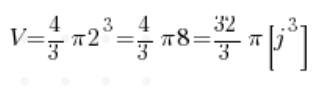
No i mamy odpowiedź, nie ruszając nawet całek 🙂



2 Komentarzy
Tomasz
No więc w końcówce pokazujesz genialnie jak umiesz program gimnazjum… pierwszy raz w życiu widzę, że 4*8 jest równe 16… już szybciej jest wszystko całką policzyć i wychodzi w 2 linijkach…
Krystian Karczyński
Faktycznie, na końcu był błąd rachunkowy, dzięki za wskazanie, poprawiłem.