In the tougher problems on definite integrals, it’s always good to stay sharp – a task that seems super hard can be cracked with a simple formula from middle school.
Problem on the Volume of a Solid of Revolution
Let’s say we need to calculate the volume of a solid formed by rotating a curve:
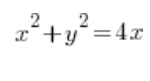
spinning (okay, let’s say “rotating”) around the OX axis. A few tidy moves known from high school…
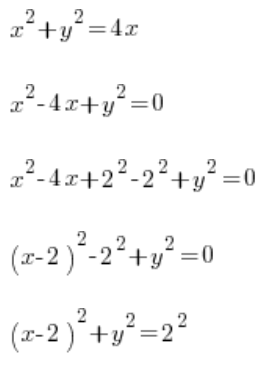
…and we realize that our curve is just a little circle with the center at point (2,0) and radius 2. What now? We derive y from the formula and push forward with the definite integral: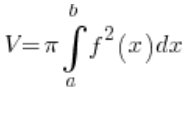 
?
Solution
No… Let’s pause for a moment. Take a deep breath. Think. A little circle… It rotates… What will result from such rotation? Obviously, a sphere. We know the formula for the volume of a sphere from middle school:
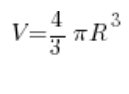
We already know the radius (it’s two), which means:
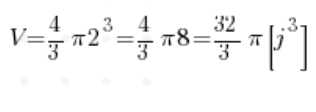
And there we have the answer, without even touching integrals 🙂
