W tym poście zbadam różniczkowalność funkcji:
f\left( x \right)=x\cdot \left| x \right|Po przerobieniu wraz ze mną tego pouczającego przykładu dowiesz się:
- jak podejść w ogóle do wartości bezwzględnej w różnych przykładach (niekoniecznie tylko z pochodnych);
- jak się bada, czy pochodna istnieje.
A dla nielubiących czytać nagrałem video:
Na początek przypomnij sobie podstawy:
Co to w ogóle jest różniczkowalność?
- funkcja jest „różniczkowalna” w jakimś punkcie, kiedy ma pochodną w tym punkcie
- funkcja ma pochodną w tym punkcie, jeżeli jej pochodne prawo- i lewostronna są równe w tym punkcie
- funkcja jest „różniczkowalna” w jakimś przedziale, kiedy jest różniczkowalna w każdym punkcie tego przedziału
- „zbadać różniczkowalność” – to znaczy określić, gdzie funkcja jest różniczkowalna (w jakich punktach/przedziałach), a gdzie nie jest
Więcej podbudowy teoretycznej znajdziesz w moich „Wykładach”:
Badanie istnienia pochodnej funkcji
W skrócie: w zadaniu chodzi o to, żeby sprawdzić, w jakich punktach funkcja f\left( x \right)=x\cdot \left| x \right| ma pochodną.
O co chodzi z tą wartością bezwzględną?
Na ten temat możesz poczytać sobie więcej tutaj:
Jak poradzić sobie z wartościami bezwzględnymi?
W skrócie: wartość bezwzględna „rozbija” na ogół wzór funkcji na dwa przypadki.
Do roboty, krok po kroku
1. Radzę sobie z wartością bezwzględną
Mamy funkcję: f\left( x \right)=x\cdot \left| x \right|.
Ponieważ w zadaniu jest wartość bezwzględna, musisz rozbić je na przypadki, zgodnie z ogólnym schematem wartości bezwzględnej:
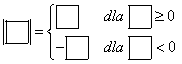
Określasz, jak wyglądać będzie funkcja w zależności od przedziałów x.
Brzmi to strasznie zawile, ale w przypadku naszej prościutkiej funkcji (wartość bezwzględna jest liczona po prostu z x), będziesz miał:
f\left( x \right)=x\left| x \right|=x\cdot x={{x}^{2}}, ale tylko dla x\ge 0.
f\left( x \right)=x\left| x \right|=x\cdot \left( -x \right)=-{{x}^{2}}, ale tylko dla x<0
UWAGA: Rozbijanie funkcji na przypadki w sytuacji, gdy w jej wzorze jest wartość bezwzględna, opisałem na kilku przykładach w innym artykule, jeśli zgubiłeś się w tym momencie, to zapraszam:
Jak poradzić sobie z wartościami bezwzględnymi w całkach (i nie tylko)
Możesz to podsumować ładnym wzorem:
f\left( x \right)=x\left| x \right|=\left\{ \begin{matrix}& {{x}^{2}}\quad \ dla\ x\ge 0 \\& -{{x}^{2}}\ \ \,dla\ x<0 \end{matrix} \right.2. Określam różniczkowalność funkcji
Mam funkcję:
f\left( x \right)=\left\{ \begin{matrix}& {{x}^{2}}\quad \ dla\ x\ge 0 \\& -{{x}^{2}}\ \ \,dla\ x<0 \end{matrix} \right.Czas na przejście do badania jej różniczkowalności. „Zbadać różniczkowalność” to znaczy: sprawdzić, gdzie funkcja posiada pochodną (dla jakich x), a gdzie nie.
Sam rzut oka na wzór funkcji podpowiada nam, gdzie ewentualnie moglibyśmy mieć jakieś wątpliwości.
We wszystkich punktach x, z wyjątkiem 0, mamy do czynienia z ładnymi wyrażeniami x^2, albo -x^2
Oczywiście pochodne w tych punktach istnieją i są równe odpowiednio 2x, albo -2x, zgodnie z elementarnymi wzorami na pochodne.
Jedyny problem, to kwestia, czy pochodna istnieje w punkcie x=0.
Trzeba zauważyć, że funkcja „na lewo” od tego punktu (bardziej fachowo: w dowolnym lewostronnym otoczeniu tego punktu) ma inny wzór ( -x^2), niż „na prawo” od tego punktu ( x^2).
Pochodna funkcji w punkcie {{x}_{0}}, jak wiadomo, to nic innego, jak pewna granica:
\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{f\left( {{x}_{0}}+\Delta x \right)-f\left( {{x}_{0}} \right)}{\Delta x}…a granica w punkcie istnieje wtedy, kiedy granice lewo- i prawostronna funkcji w tym punkcie są sobie równe.
W tym jednym, jedynym punkcie funkcji zachodzi ryzyko, że granice lewo- i prawostronna funkcji nie będą równe – bo przy ich obliczaniu użyjemy zupełnie innych wzorów na funkcję.
W tym jednym, jedynym punkcie pochodną funkcji nie obliczymy ze znanego wzoru na pochodną z x^2, trzeba będzie wysilić się i zrobić to z definicji.
Po podstawieniu punktu {{x}_{0}}=0 do definicji otrzymasz:
{f}'\left( 0 \right)=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{f\left( 0+\Delta x \right)-f\left( \Delta x \right)}{\Delta x}Niestety na tym etapie nie można powiedzieć, czy f\left( x \right)={{x}^{2}}, czy f\left( x \right)=-{{x}^{2}}, bo nie wiemy, czy tej funkcji argumentem jest liczba ujemna, czy nieujemna. \Delta x może przecież dążyć do zera i być dodatnie, albo może dążyć do zera i być ujemne.
Musisz rozpatrzyć oba przypadki i policzyć granice jednostronne.
Lewostronną, czyli przy \Delta x dążącym do zera, ale ujemnym. Korzystasz ze wzoru f\left( x \right)=-{{x}^{2}}.
\underset{\Delta x\to {{0}^{-}}}{\mathop{\lim }}\,\frac{f\left( 0+\Delta x \right)-f\left( 0 \right)}{\Delta x}=\underset{\Delta x\to {{0}^{-}}}{\mathop{\lim }}\,\frac{-{{\left( 0+\Delta x \right)}^{2}}-{{ 0}^{2}} }{\Delta x}=\underset{\Delta x\to {{0}^{-}}}{\mathop{\lim }}\,\frac{-{{\left( \Delta x \right)}^{2}}}{\Delta x}= =\underset{\Delta x\to {{0}^{-}}}{\mathop{\lim }}\,\left( -\Delta x \right)=0Prawostronną, czyli przy \Delta x dążącym do zera, ale dodatnim. Korzystasz ze wzoru f\left( x \right)={{x}^{2}}.
\underset{\Delta x\to {{0}^{+}}}{\mathop{\lim }}\,\frac{f\left( 0+\Delta x \right)-f\left( 0 \right)}{\Delta x}=\underset{\Delta x\to {{0}^{+}}}{\mathop{\lim }}\,\frac{{{\left( 0+\Delta x \right)}^{2}}-{{0}^{2}}}{\Delta x}=\underset{\Delta x\to {{0}^{+}}}{\mathop{\lim }}\,\frac{{{\left( \Delta x \right)}^{2}}}{\Delta x}= =\underset{\Delta x\to {{0}^{+}}}{\mathop{\lim }}\,\left( \Delta x \right)=0Wniosek
Pochodne lewo- i prawostronne w punkcie x=0 wyszły równe. Zatem pochodna w tym punkcie istnieje. Zatem funkcja jest różniczkowalna w tym punkcie. Skoro jest różniczkowalna także w każdym innym punkcie…
Odpowiedź
Funkcja jest różniczkowalna w całej swojej dziedzinie. W skrócie: funkcja jest różniczkowalna.
Sprawdź to sam na wykresie funkcji
Na koniec zapraszam Cię do samodzielnego sprawdzenia wyniku (przed zabawą z wykresem musisz zainstalować darmowy program Wolfram CDF Player ).
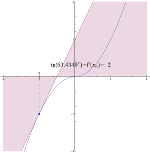
Samodzielnie możesz ustalać współrzędną x_0 (w granicach od -2 do 2). Pochodna w tym punkcie, to z definicji tangens kąta pomiędzy styczną tej funkcji w tym punkcie, a osią OX.
Zwróć uwagę, że zbliżając się do 0 zarówno z lewej, jak i prawej strony, tangensy tego kąta dążą do tej same liczby (do 0). Oznacza to, że funkcja ma w tym punkcie pochodną, czyli jest w nim różniczkowalna.




kacper
„Po podstawieniu punktu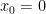 do definicji otrzymasz: ” wydaje mi się, że po tym zdaniu na obrazu jest błąd w definicji pochodnej.
do definicji otrzymasz: ” wydaje mi się, że po tym zdaniu na obrazu jest błąd w definicji pochodnej.