व्युत्पन्नों के सूत्र
विषय: उलटे फ़ंक्शन की व्युत्पन्न की प्रमेय। प्रमेय का उपयोग करके कई व्युत्पन्न सूत्र निकालना।
सारांश
हमारे लेक्चर में, हम उलटे फ़ंक्शन की व्युत्पन्न की इस दिलचस्प प्रमेय में गोता लगाएंगे। हम इसे साबित करेंगे और देखेंगे कि इसे कैसे इस्तेमाल करके व्युत्पन्न के कई सूत्रों को निकाला जा सकता है। इस प्रमेय के बिना, इन सूत्रों को निकालना (जैसा कि हमने पिछले लेक्चर में सीधे परिभाषाओं से किया था) काफी कठिन होता, हल्के शब्दों में कहें तो – एक मुश्किल काम।
इस प्रमेय पर चर्चा करने से पहले, यह जानना अच्छा होगा कि उलटा फ़ंक्शन क्या है, क्यों ![]() का उलटा फ़ंक्शन
का उलटा फ़ंक्शन ![]() है, और क्यों इस मामले में हमें तर्कों की श्रेणी को सीमित करना पड़ता है जैसे कि
है, और क्यों इस मामले में हमें तर्कों की श्रेणी को सीमित करना पड़ता है जैसे कि ![]() …
…
विश्वविद्यालय स्तर की गणितीय विश्लेषण में, इस प्रमेय का उपयोग करके सूत्रों को निकालना एक बह ुत ही आम कार्य है, इसलिए यह लेक्चर एक दिन आपके अकादमिक जीवन में काम आ सकता है।
मैंने फिचेनहोल्ज़ की किताब से प्रमेय और प्रमाण लिया है, इसमें यहां-वहां बदलाव किए हैं, टाइपिंग की गलतियों को सुधारा है, और कुछ अन्य परिवर्तन किए हैं।
उलटे फ़ंक्शन की व्युत्पन्न की प्रमेय
यदि फ़ंक्शन ![]() का एक उलटा फ़ंक्शन होता है
का एक उलटा फ़ंक्शन होता है ![]() , और बिंदु
, और बिंदु ![]() पर इसकी एक सीमित और शून्य से भिन्न व्युत्पन्न
पर इसकी एक सीमित और शून्य से भिन्न व्युत्पन्न ![]() होती है, तो संबंधित बिंदु
होती है, तो संबंधित बिंदु ![]() पर उलटे फ़ंक्शन की व्युत्पन्न
पर उलटे फ़ंक्शन की व्युत्पन्न 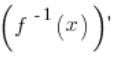 मौजूद होती है और इसकी कीमत
मौजूद होती है और इसकी कीमत ![]() पर
पर 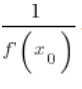 होती है।
होती है।
इस प्रतीकों की श्रृंखला से भ्रमित हो रहे हैं? शुरुआत में, यह बहुत संभव है, लेकिन आइए हम कुछ सरल और विशिष्ट उदाहरणों के म.
उदाहरण 1
यदि कोई फ़ंक्शन
के पास उल्टा फ़ंक्शन हो
,
1. हम फ़ंक्शन ![]() को अंतराल
को अंतराल ![]() में लेते हैं।
में लेते हैं।
2. इसका उल्टा फ़ंक्शन मौजूद है और वह है ![]() – मैं इस x अंतराल की सीमा का कारण और व्याख्या नहीं कर रहा हूँ, माफ़ कीजिए…
– मैं इस x अंतराल की सीमा का कारण और व्याख्या नहीं कर रहा हूँ, माफ़ कीजिए…
और बिंदु
पर इसका सीमित और शून्य से भिन्न व्युत्पन्न है
,
3. हम बिंदु ![]() लेते हैं। फ़ंक्शन
लेते हैं। फ़ंक्शन ![]() का व्युत्पन्न मौजूद है (
का व्युत्पन्न मौजूद है (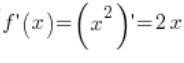 ) और बिंदु
) और बिंदु ![]() पर इसका मान शून्य से भिन्न है (
पर इसका मान शून्य से भिन्न है (![]() )।
)।
तो उस बिंदु के अनुरूप
बिंदु
4. बिंदु ![]() के अनुरूप बिंदु
के अनुरूप बिंदु ![]() वह है जो बिंदु
वह है जो बिंदु ![]() के लिए फ़ंक्शन
के लिए फ़ंक्शन ![]() का मान है, अर्थात्
का मान है, अर्थात् 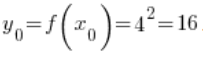 ।
।
तो हमारे उदाहरण में:
![]()
उल्टे फ़ंक्शन का व्युत्पन्न
मौजूद है
5. वास्तव में, उल्टा फंक्शन है ![]() , इसका डेरिवेटिव है:
, इसका डेरिवेटिव है: 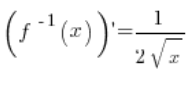 (मूल डेरिवेटिव सूत्रों से) और बिंदु
(मूल डेरिवेटिव सूत्रों से) और बिंदु ![]() पर बिल्कुल मौजूद है और बराबर है:
पर बिल्कुल मौजूद है और बराबर है:
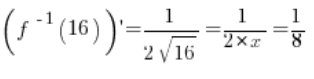
और इसका मूल्य बिंदु
पर है
.
6. वास्तव में, बिंदु 5 में गणना की गई 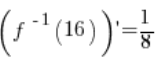 के बराबर है:
के बराबर है:
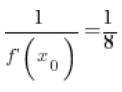 (
(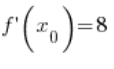 – मैंने इसे बिंदु 3 में गणना की।)
– मैंने इसे बिंदु 3 में गणना की।)
तो यह सिद्धांत “काम करता है” 🙂
उदाहरण 2
यदि कोई फ़ंक्शन
के पास एक उल्टा फ़ंक्शन है
,
1. आइए एक्सपोनेंशियल फ़ंक्शन लेते हैं ![]()
2. इसका उल्टा फ़ंक्शन मौजूद है जो है ![]() – यह स्कूल में पढ़ाया गया था, इसलिए फिर से नहीं समझाऊंगा (लॉगारिदमिक और एक्सपोनेंशियल फ़ंक्शंस एक दूसरे के उल्टे होते हैं)
– यह स्कूल में पढ़ाया गया था, इसलिए फिर से नहीं समझाऊंगा (लॉगारिदमिक और एक्सपोनेंशियल फ़ंक्शंस एक दूसरे के उल्टे होते हैं)
और बिंदु
पर इसका सीमित और शून्य से अलग डेरिवेटिव
होता है,
3. आइए बिंदु ![]() लेते हैं। फ़ंक्शन
लेते हैं। फ़ंक्शन ![]() का डेरिवेटिव मौजूद है (
का डेरिवेटिव मौजूद है (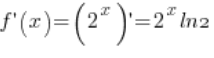 – बुनियादी डेरिवेटिव फॉर्म
ुले) और बिंदु
– बुनियादी डेरिवेटिव फॉर्म
ुले) और बिंदु ![]() पर इसका मान शून्य से अलग है (
पर इसका मान शून्य से अलग है (![]() )।
)।
तो उसके अनुरूप बिंदु
में बिंदु
4. बिंदु ![]() के अनुरूप बिंदु
के अनुरूप बिंदु ![]() वह मान है जो फ़ंक्शन
वह मान है जो फ़ंक्शन ![]() का है बिंदु
का है बिंदु ![]() में, यानी
में, यानी 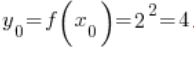 ।
।
इसका मतलब है:
![]()
उल्टे फ़ंक्शन का डेरिवेटिव
मौजूद है
5. सच में, उल्टा फ़ंक्शन है ![]() , इसका डेरिवेटिव बराबर है:
, इसका डेरिवेटिव बराबर है: 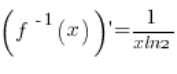 (बुनियादी डेरिवेटिव फॉर्मुलों से)। बिंदु
(बुनियादी डेरिवेटिव फॉर्मुलों से)। बिंदु ![]() पर डेरिवेटिव मौजूद है और बराबर है:
पर डेरिवेटिव मौजूद है और बराबर है:
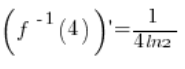
और इसकी कीमत बिंदु
में बराबर है
।
6. सच में, 5वें बिंदु में गणना की गई 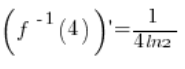 बराबर है:
बराबर है:
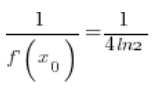 (
(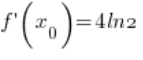 – मैंने इसे 3वें बिंदु में गणना किया था।)
– मैंने इसे 3वें बिंदु में गणना किया था।)
तो सिद्धांत फिर से “काम करता है” 🙂
उलटे फंक्शन के डेरिवेटिव पर प्रमेय का प्रमाण
हम इस प्रमेय को साबित करेंगे, बिंदु पर फंक्शन के डेरिवेटिव के ज्यामितीय व्याख्या का संदर्भ लेकर। जैसा कि हम जानते हैं, बिंदु पर फंक्शन के डेरिवेटिव का मान उस बिंदु पर फंक्शन के ग्राफ की स्पर्शरेखा की ढलान के तनजेंट के बराबर होता है।
ग्राफ पर यह कुछ इस प्रकार दिखाई देगा:
 बिंदु
बिंदु ![]() में डेरिवेटिव का मान हमने पहले के व्याख्यानों में कोण
में डेरिवेटिव का मान हमने पहले के व्याख्यानों में कोण ![]() के तनजेंट के रूप में परिभाषित किया था।
के तनजेंट के रूप में परिभाषित किया था।
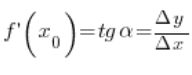
अब हम एक रोचक बात पर ध्यान दें: ![]() के उलटे फंक्शन का ग्राफ ठीक उसी ग्राफ पर प्रस्तुत किया जा सकता है, बस याद रखें कि इसे “उल्टा” पढ़ा जाता है – अर्थात जैसे कि हम y के मानों को x के मानों से जोड़
ते हैं (इसलिए उलटे फंक्शन के पैरामीटर्स की वृद्धि
के उलटे फंक्शन का ग्राफ ठीक उसी ग्राफ पर प्रस्तुत किया जा सकता है, बस याद रखें कि इसे “उल्टा” पढ़ा जाता है – अर्थात जैसे कि हम y के मानों को x के मानों से जोड़
ते हैं (इसलिए उलटे फंक्शन के पैरामीटर्स की वृद्धि ![]() है, और उनके मानों की वृद्धि
है, और उनके मानों की वृद्धि ![]() है):
है):
 देखिए, उस बिंदु पर उलटे फंक्शन के डेरिवेटिव का मूल्य
देखिए, उस बिंदु पर उलटे फंक्शन के डेरिवेटिव का मूल्य ![]() के बराबर है:
के बराबर है:
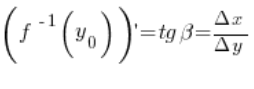
इससे स्पष्ट है कि फंक्शन और उसके उलटे फंक्शन के डेरिवेटिव के मूल्य उसी समकोण त्रिकोण में कोणों के तनजेंट होते हैं।
और समकोण त्रिकोण में कोणों के तनजेंट (जैसा कि हम माध्यमिक विद्यालय से याद करते हैं) निम्नलिखित संबंध से जुड़े होते हैं:
![]()
इसका मतलब है कि (अगर हम ![]() से दोनों तरफ भाग करते हैं):
से दोनों तरफ भाग करते हैं):
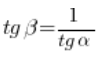
और इससे हमारे प्रमेय का निष्कर्ष निकलता है, अर्थात:
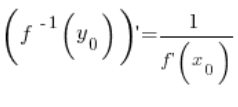
🙂
प्रमाण का अंत
उलटे फंक्शन के डेरिवेटिव पर प्रमेय का उपयोग करके डेरिवेटिव के सूत्रों की व्युत्पत्ति
उदाहरण 3
फंक्शन ![]() के डेरिवेटिव का सूत्र व्युत्पन्न करें।
के डेरिवेटिव का सूत्र व्युत्पन्न करें।
जिस सूत्र को हमें व्युत्पन्न करना है, वह है: 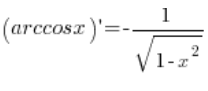 ।
।
हमारा फंक्शन f(x) arccosx है। इसका उलटा फंक्शन है ![]() । उलटे फंक्शन का डेरिवेटिव है
। उलटे फंक्शन का डेरिवेटिव है 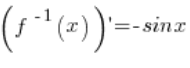 ।
।
उलटे फंक्शन के डेरिवेटिव पर प्रमेय के अनुसार बिंदु ![]() में उलटे फंक्शन के डेरिवेटिव का मूल्य बिंदु
में उलटे फंक्शन के डेरिवेटिव का मूल्य बिंदु ![]() में फंक्शन के डेरिवेटिव के उलटे के बराबर होता है:
में फंक्शन के डेरिवेटिव के उलटे के बराबर होता है:
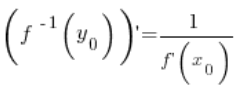
इसका मतलब है कि किसी भी बिंदु ![]() में:
में:
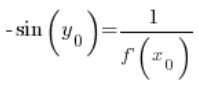
परिवर्तन के बाद:
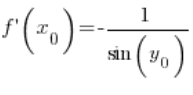
त्रिकोणमितीय एकता का उपयोग करते हुए हम व्युत्पन्न कर सकते हैं कि: 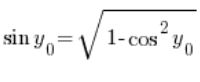 , इसलिए हमारे पास है:
, इसलिए हमारे पास है:
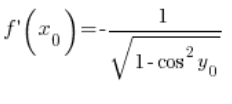
अब ध्यान दें: ![]() यह बिंदु
यह बिंदु ![]() में फंक्शन
में फंक्शन ![]() का मूल्य है, यानी
का मूल्य है, यानी 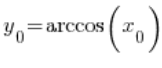 । इसलिए:
। इसलिए:
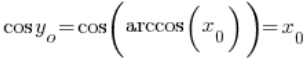 – क्योंकि कोसाइन और आर्क कोसाइन उलटे फंक्शन हैं, इसलिए हमारे पास है:
– क्योंकि कोसाइन और आर्क कोसाइन उलटे फंक्शन हैं, इसलिए हमारे पास है:
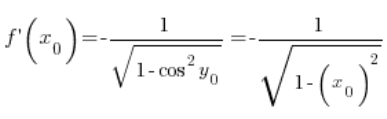 किसी भी बिंदु
किसी भी बिंदु ![]() में (बेशक, डोमेन की शर्तों का पालन करते हुए, जिसे मैंने अनदेखा किया है), इस प्रकार हमारा सूत्र
में (बेशक, डोमेन की शर्तों का पालन करते हुए, जिसे मैंने अनदेखा किया है), इस प्रकार हमारा सूत्र 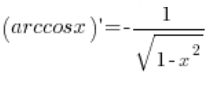 इस तरह से सिद्ध हुआ है।
इस तरह से सिद्ध हुआ है।
उदाहरण 4
फंक्शन ![]() के डेरिवेटिव का सूत्र निकालें।
के डेरिवेटिव का सूत्र निकालें।
निकालने वाला सूत्र यह है: 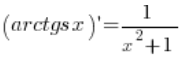 ।
।
हमारा फंक्शन f(x) arctgx है। इसका उलटा फंक्शन ![]() है। उलटे फंक्शन का डेरिवेटिव
है। उलटे फंक्शन का डेरिवेटिव 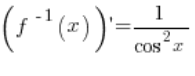 है।
है।
उलटे फंक्शन के डेरिवेटिव पर प्रमेय के अनुसार बिंदु ![]() में उलटे फंक्शन के डेरिवेटिव का मूल्य बिंदु
में उलटे फंक्शन के डेरिवेटिव का मूल्य बिंदु ![]() में फंक्शन के डेरिवेटिव के उलटे के बराबर होता है:
में फंक्शन के डेरिवेटिव के उलटे के बराबर होता है:
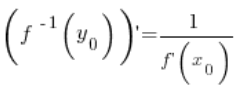
इसलिए किसी भी बिंदु ![]() में:
में:
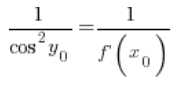
परिवर्तन के बाद:
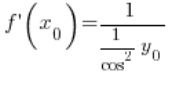
त्रिकोणमितीय एकता का उपयोग करके हम इसे आगे परिवर्तित कर सकते हैं:
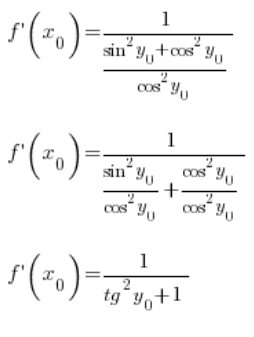
अब ध्यान दें: ![]() बिंदु
बिंदु 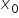 में फंक्शन
में फंक्शन ![]() का मान है, यानी
का मान है, यानी 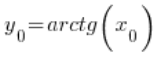 . इसलिए:
. इसलिए: 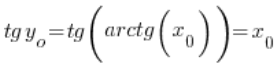 – क्योंकि टैंजेंट और आर्कटैंजेंट उलटे फंक्शन हैं, हमारे पास इस प्रकार है:
– क्योंकि टैंजेंट और आर्कटैंजेंट उलटे फंक्शन हैं, हमारे पास इस प्रकार है:
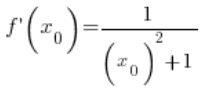 किसी भी बिंदु
किसी भी बिंदु ![]() में (जो स्पष्टतः डोमेन की शर्तों को पूरा करता है, जिसे मैंने ध्यान में नहीं रखा), इसलिए हमारा सूत्र
में (जो स्पष्टतः डोमेन की शर्तों को पूरा करता है, जिसे मैंने ध्यान में नहीं रखा), इसलिए हमारा सूत्र 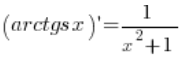 इस तरीके से सिद्ध हो गया है।
इस तरीके से सिद्ध हो गया है।
समापन
इस पोस्ट को लिखने के लिए मैंने इसका उपयोग किया…
1. “रियल वर्ल्ड मैथमेटिक्स.” आंद्रे द्वायने। प्रकाशन 2022।
पूर्वरूप से डिफ़िनिशन के आधार पर पॉच की जाने वाली सूत्रों को बाहर लाने के लिए यहाँ क्लिक करें <–
पॉच की संपत्तियों को कैसे सिद्ध कर सकते हैं, यहाँ क्लिक करें (अगला लेख) –>
पॉच के बारे में व्याख्यानों के मुख्य पृष्ठ पर वापस जाने के लिए क्लिक करें

