导数公式
主题:反函数的导数定理。应用该定理推导出几个导数公式。
摘要
在我们的讲座中,我们将深入探讨反函数导数的这个有趣定理。我们将证明它,并看看如何使用它来推导出一系列导数公式。如果没有这个定理,推导这些公式(就像我们在上一讲中直接从定义中做的那样)可能会是一件相当困难的事情。
在处理这个定理之前,最好先知道什么是反函数,为什么![]() 的反函数是
的反函数是![]() ,以及为什么在这种情况下我们必须限制自己使用像
,以及为什么在这种情况下我们必须限制自己使用像![]() 这样的参数范围……
这样的参数范围……
在大学级别的数学分析中,使用这个定理来推导公式是一个非常常见的任务,所以这堂讲座有可能在你的学术生涯中派上用场。
我引用并修改了费希滕霍尔茨的书中的定理和证明,对其中的一些地方进行了调整、修正了打字错误,并做了一些更改。
反函数的导数定理
如果函数![]() 有一个反函数
有一个反函数 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
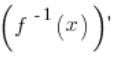
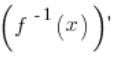
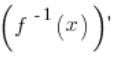
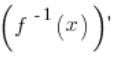
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
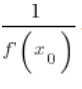
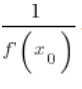
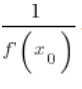
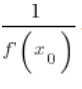
这一串符号让你感到困惑吗?一开始很可能是的,但让我们通过几个简单具体的例子深入理解这个定理。
例子 1
如果函数
有一个逆函数 ,
1. 我们取函数 ![]()
![]()
![]()
![]()
![]()
![]()
2. 它的逆函数存在,是 ![]()
![]()
![]()
并且在点
它有一个有限且非零的导数 ,
3. 我们取点 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
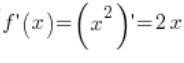
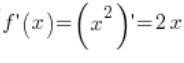
![]()
![]()
![]()
![]()
![]()
那么在对应点
的点
4. 对应于点 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
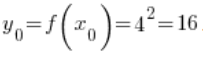
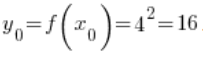
所以在我们的例子中:
![]()
![]()
![]()
逆函数的导数
存在
5. 确实,逆函数是 ![]()
![]()
![]()
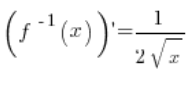
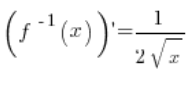
![]()
![]()
![]()
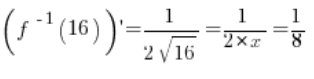
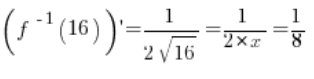
其值在点
等于 。
6. 确实,在第 5 点计算的 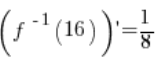
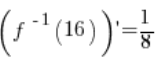
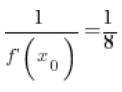
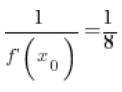
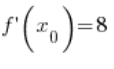
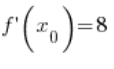
所以定理“有效” 🙂
例子 2
如果函数
有一个逆函数 ,
1. 我们取指数函数 ![]()
![]()
![]()
![]()
2. 它的逆函数存在,是 ![]()
![]()
![]()
并且在点
它有一个有限且非零的导数 ,
3. 我们取点 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
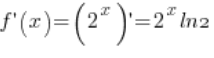
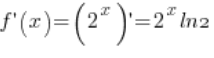
![]()
![]()
![]()
![]()
![]()
![]()
那么在对应点
的点
4. 对应于点 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
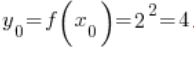
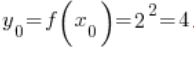
所以:
![]()
![]()
![]()
存在逆函数的导数
5. 的确,逆函数是 ![]()
![]()
![]()
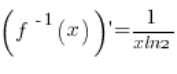
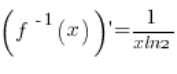
![]()
![]()
![]()
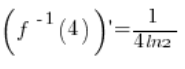
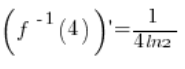
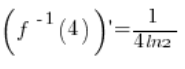
其值在点
等于 。
6. 的确,在第5点计算的 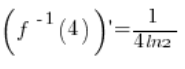
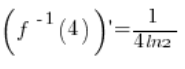
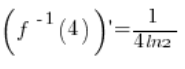
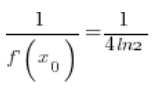
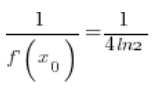
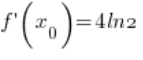
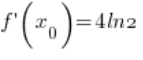
所以,定理再次“有效” :)
逆函数导数定理的证明
我们将通过引用函数在点上导数的几何解释来证明这个定理。我们记得,在点上函数的导数值是该点函数图形切线的斜率的正切。
在图形上看起来是这样的:


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
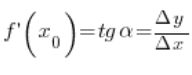
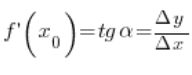
现在让我们注意到一个有趣的事实:逆函数 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
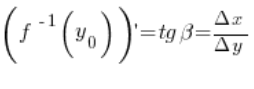
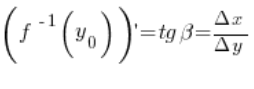
因此,我们看到函数和其逆函数的导数值是同一个直角三角形中角的正切。
而直角三角形中角的正切(我们从高中记得)与以下关系相连:
![]()
![]()
所以(在双方
都除以 ![]()
![]()
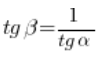
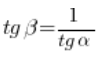
由此得出我们定理的结论,即:
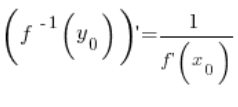
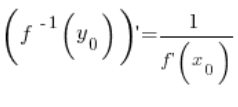
🙂
证明结束
利用逆函数导数定理推导导数公式
示例 3
推导函数 ![]()
![]()
![]()
我们需要推导的公式是: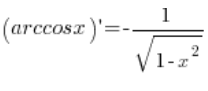
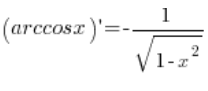
我们的函数 f(x) 是 arccosx 函数。它的逆函数是 ![]()
![]()
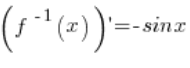
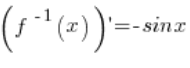
根据逆函数导数定理,逆函数在点 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
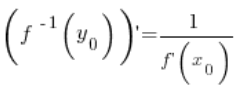
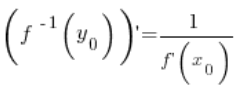
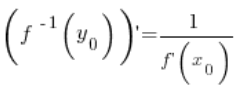
即在任意点 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
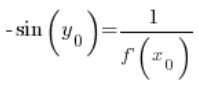
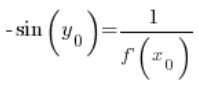
经过转换:
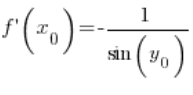
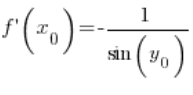
利用三角恒等式,我们可以推导出: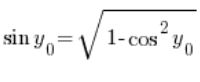
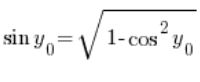
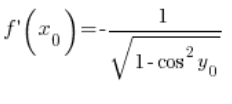
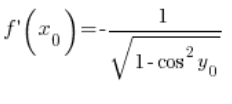
现在注意:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
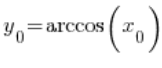
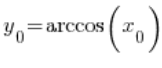
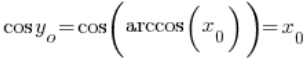
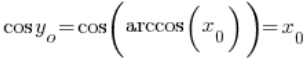
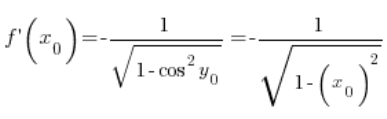
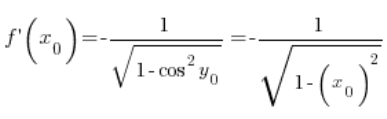
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
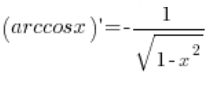
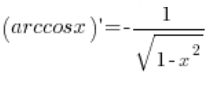
示例 4
推导函数 ![]()
![]()
![]()
我们需要推导的公式是: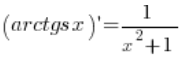
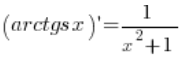
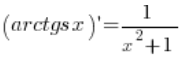
我们的函数 f(x) 是 arctgx 函数。它的逆函数是 ![]()
![]()
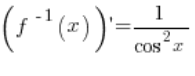
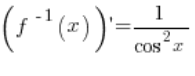
根据逆函数导数定理,逆函数在点 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
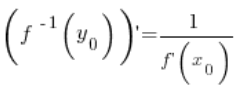
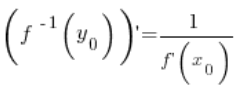
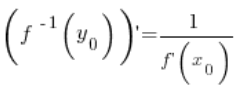
即在任意点 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
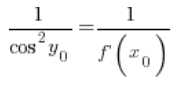
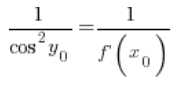
经过转换:
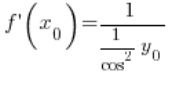
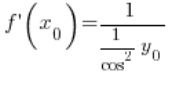
利用三角恒等式,我们可以进一步转换:
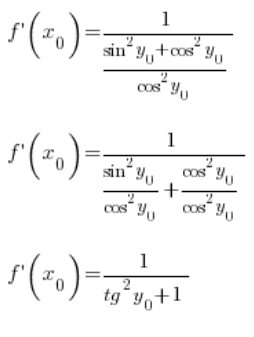
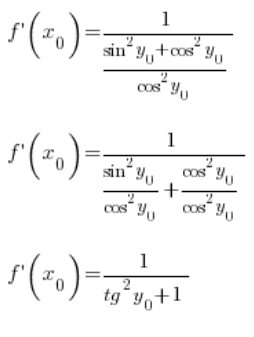
现在注意:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
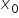
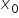
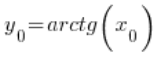
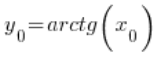
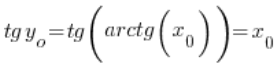
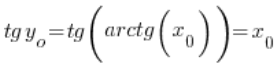
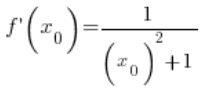
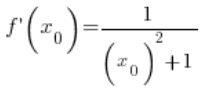
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
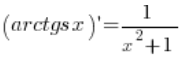
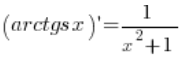
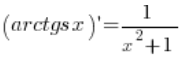
结束
撰写此文时,我参考了…
1. “微积分学. 第一卷.” G.M. Fichtenholz. 1966年出版。

