Formeln für Ableitungen
Thema: Der Satz über die Ableitung der Umkehrfunktion. Anwendung des Satzes zur Ableitung einiger Ableitungsformeln.
Zusammenfassung
In dieser Vorlesung werden wir uns mit dem Satz über die Ableitung der Umkehrfunktion befassen, ihn beweisen und sehen, wie er zur Bestimmung verschiedener Ableitungsformeln verwendet werden kann. Ohne diesen Satz (zum Beispiel direkt aus der Definition, wie in der vorherigen Vorlesung) wäre es, vorsichtig ausgedrückt – schwierig.
Leider muss man, bevor man sich dem Satz nähert, wissen, was eine Umkehrfunktion ist, warum die Funktion ![]() die Umkehrfunktion zu
die Umkehrfunktion zu ![]() ist und warum wir uns in diesem Fall auf einen Argumentbereich wie
ist und warum wir uns in diesem Fall auf einen Argumentbereich wie ![]() beschränken müssen…
beschränken müssen…
Das Ableiten von Formeln mithilfe des Satzes über die Ableitung der Umkehrfunktion ist eine recht häufige Aufgabe in der mathematischen Analyse an der Universität, also könnte dir diese Vorlesung in deinen akademischen Kämpfen nützlich sein.
Den Satz und den Beweis stelle ich unter Verwendung des Buches von Fichtenholz vor, indem ich ihn erweitere, einschränke, Tippfehler korrigiere und an einigen Stellen überarbeite.
Der Satz über die Ableitung der Umkehrfunktion
Wenn die Funktion ![]() eine Umkehrfunktion
eine Umkehrfunktion ![]() besitzt, und im Punkt
besitzt, und im Punkt ![]() eine endliche und von null verschiedene Ableitung
eine endliche und von null verschiedene Ableitung ![]() hat, dann existiert im entsprechenden Punkt
hat, dann existiert im entsprechenden Punkt ![]()
![]() die Ableitung der Umkehrfunktion
die Ableitung der Umkehrfunktion 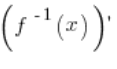 , und ihr Wert im Punkt
, und ihr Wert im Punkt ![]() entspricht
entspricht 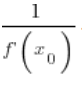 .
.
Unverständliche Zeichenfolge? Am Anfang sehr möglich, lasst uns also in dieses Theorem eintauchen, indem wir zwei einfache, konkrete Beispiele verwenden.
Beispiel 1
Wenn die Funktion
eine Umkehrfunktion
besitzt,
1. Nehmen wir die Funktion ![]() im Intervall
im Intervall ![]() .
.
2. Die Umkehrfunktion dazu existiert und ist gleich ![]() – ich erkläre nicht mehr, warum und wozu diese Einschränkung im Intervall x, sorry…
– ich erkläre nicht mehr, warum und wozu diese Einschränkung im Intervall x, sorry…
und im Punkt
eine endliche und von null verschiedene Ableitung
hat,
3. Nehmen wir den Punkt ![]() . Die Ableitung der Funktion
. Die Ableitung der Funktion ![]() existiert (
existiert (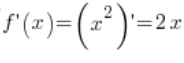 ) und ihr Wert im Punkt
) und ihr Wert im Punkt ![]() ist von null verschieden (
ist von null verschieden (![]() ).
).
entsprechend dem Punkt
ist der Punkt
4. Der dem Punkt ![]() entsprechende Punkt
entsprechende Punkt ![]() ist der dem Punkt
ist der dem Punkt ![]() entsprechende Wert der Funktion
entsprechende Wert der Funktion ![]() , also
, also 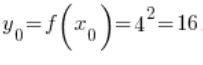 .
.
In unserem Beispiel also:
![]()
existiert die Ableitung der Umkehrfunktion
5. In der Tat, die Umkehrfunktion ist ![]() , ihre Ableitung ist:
, ihre Ableitung ist: 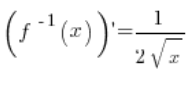 (aus den Grundformeln für Ableitungen) und im Punkt
(aus den Grundformeln für Ableitungen) und im Punkt ![]() existiert sie definitiv und ist gleich:
existiert sie definitiv und ist gleich:
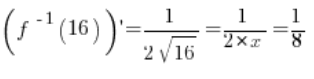
und ihr Wert im Punkt
entspricht
.
6. Tatsächlich ist die in Punkt 5 berechnete 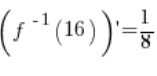 gleich:
gleich:
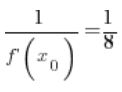 (
(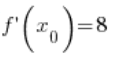 – das habe ich in Punkt 3 berechnet.)
– das habe ich in Punkt 3 berechnet.)
Also funktioniert der Satz 🙂
Beispiel 2
Wenn die Funktion
eine Umkehrfunktion
besitzt,
1. Nehmen wir die Exponentialfunktion ![]() .
.
2. Die Umkehrfunktion dazu existiert und ist gleich ![]() – das war in der Schule, ich erkläre auch nicht (die logarithmische und die Exponentialfunktion sind Umkehrfunktionen zueinander).
– das war in der Schule, ich erkläre auch nicht (die logarithmische und die Exponentialfunktion sind Umkehrfunktionen zueinander).
und im Punkt
hat sie eine endliche und von null verschiedene Ableitung
,
3. Nehmen wir den Punkt ![]() . Die Ableitung der Funktion
. Die Ableitung der Funktion ![]() existiert (
existiert (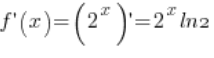 – Grundformeln der Ableitung) und ist im Punkt
– Grundformeln der Ableitung) und ist im Punkt ![]() von null verschieden (
von null verschieden (![]() ).
).
dann existiert im entsprechenden Punkt

die Ableitung der Umkehrfunktion,
4. Der dem Punkt ![]() entsprechende Punkt
entsprechende Punkt ![]() ist der Wert der Funktion
ist der Wert der Funktion ![]() im Punkt
im Punkt ![]() , also
, also 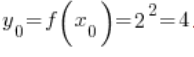 .
.
Also:
![]()
existiert die Ableitung der Umkehrfunktion
5. Tatsächlich ist die Umkehrfunktion ![]() , ihre Ableitung ist:
, ihre Ableitung ist: 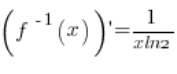 (aus den Grundformeln für Ableitungen). Im Punkt
(aus den Grundformeln für Ableitungen). Im Punkt ![]() existiert sie und ist gleich:
existiert sie und ist gleich:
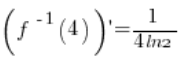
und ihr Wert im Punkt
entspricht
.
6. Tatsächlich ist die in Punkt 5 berechnete 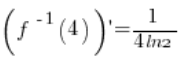 gleich:
gleich:
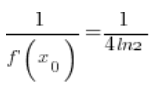 (
(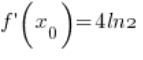 – berechnet in Punkt 3.)
– berechnet in Punkt 3.)
Also funktioniert der Satz wieder 🙂
Beweis des Satzes über die Ableitung der Umkehrfunktion
Wir werden diesen Satz beweisen, indem wir uns auf die geometrische Interpretation der Ableitung einer Funktion an einem Punkt beziehen. Wie wir uns erinnern, ist der Wert der Ableitung einer Funktion an einem Punkt der Tangens des Neigungswinkels der Tangente an die Funktionskurve an diesem Punkt.
Im Diagramm würde das so aussehen:
 Der Wert der Ableitung am Punkt
Der Wert der Ableitung am Punkt ![]() haben wir in früheren Vorlesungen als Tangens des Winkels
haben wir in früheren Vorlesungen als Tangens des Winkels ![]() definiert
definiert
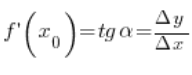
Lassen Sie uns nun etwas Interessantes bemerken: Das Diagramm der Umkehrfunktion zu ![]() kann auf genau demselben Diagramm dargestellt werden, nur dass man sich daran erinnern muss, es „umgekehrt“ zu lesen – d.h., als ob wir den y-Werten die x-Werte zuordnen (also ist die Zunahme der Argumente der Umkehrfunktion
kann auf genau demselben Diagramm dargestellt werden, nur dass man sich daran erinnern muss, es „umgekehrt“ zu lesen – d.h., als ob wir den y-Werten die x-Werte zuordnen (also ist die Zunahme der Argumente der Umkehrfunktion ![]() , und die Zunahme der entsprechenden Werte ist
, und die Zunahme der entsprechenden Werte ist ![]() ):
):
 Beachten Sie, dass der Wert der Ableitung dieser Umkehrfunktion am Punkt
Beachten Sie, dass der Wert der Ableitung dieser Umkehrfunktion am Punkt ![]() gleich ist:
gleich ist:
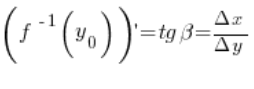
Man sieht also, dass der Wert der Ableitung der Funktion und der Wert der Ableitung ihrer Umkehrfunktion die Tangenswerte der Winkel im selben rechtwinkligen Dreieck sind.
Solche Tangenswerte von Winkeln in einem rechtwinkligen Dreieck (wie wir uns aus der Mittelschule erinnern) sind durch die Beziehung verbunden:
![]()
Also (nach dem Teilen beider Seiten durch ![]() ):
):
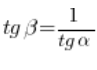
Daraus ergibt sich die Schlussfolgerung unseres Satzes, nämlich:
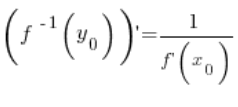
🙂
ENDE DES BEWEISES
Ableitungen mithilfe des Satzes über die Ableitung der Umkehrfunktion herleiten
Beispiel 3
Leite die Formel für die Ableitung der Funktion ![]() her.
her.
Die Formel, die wir herleiten sollen, lautet: 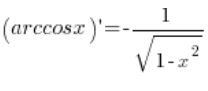 .
.
Unsere Funktion f(x) ist die Funktion arccosx. Die Umkehrfunktion dazu ist die Funktion ![]() . Die Ableitung der Umkehrfunktion ist
. Die Ableitung der Umkehrfunktion ist 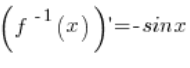 .
.
Laut dem Satz über die Ableitung der Umkehrfunktion ist der Wert der Ableitung der Umkehrfunktion an der Stelle ![]() gleich dem Kehrwert des Wertes der Ableitung der Funktion an der Stelle
gleich dem Kehrwert des Wertes der Ableitung der Funktion an der Stelle ![]() :
:
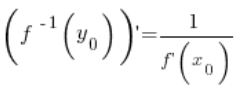
Also in jedem Punkt ![]() :
:
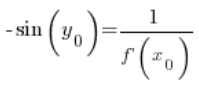
Nach Umformung:
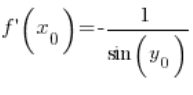
Mithilfe der trigonometrischen Identität können wir folgern, dass: 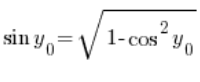 , also haben wir:
, also haben wir:
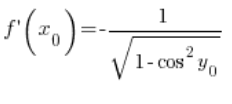
Achtung: ![]() ist der Wert der Funktion
ist der Wert der Funktion ![]() am Punkt
am Punkt ![]() , also
, also 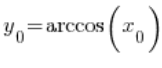 . Daher:
. Daher:
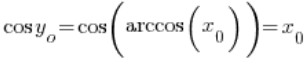 – da Kosinus und Arkuskosinus Umkehrfunktionen sind, haben wir also:
– da Kosinus und Arkuskosinus Umkehrfunktionen sind, haben wir also:
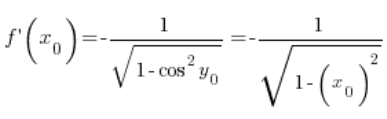 in jedem Punkt
in jedem Punkt ![]() (natürlich unter Berücksichtigung der Bedingungen des Definitionsbereichs, die ich vernachlässigt habe), somit wurde unsere Formel
(natürlich unter Berücksichtigung der Bedingungen des Definitionsbereichs, die ich vernachlässigt habe), somit wurde unsere Formel 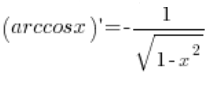 auf diese Weise nachgewiesen.
auf diese Weise nachgewiesen.
Beispiel 4
Leite die Formel für die Ableitung der Funktion ![]() her.
her.
Die Formel, die wir herleiten sollen, lautet: 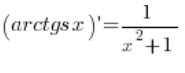 .
.
Unsere Funktion f(x) ist die Funktion arctgx. Die Umkehrfunktion dazu ist die Funktion ![]() . Die Ableitung der Umkehrfunktion ist
. Die Ableitung der Umkehrfunktion ist 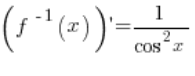 .
.
Laut dem Satz über die Ableitung der Umkehrfunktion ist der Wert der Ableitung der Umkehrfunktion an der Stelle ![]() gleich dem Kehrwert des Wertes der Ableitung der Funktion an der Stelle
gleich dem Kehrwert des Wertes der Ableitung der Funktion an der Stelle ![]() :
:
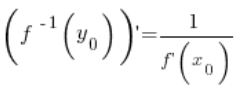
Also in jedem Punkt ![]() :
:
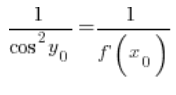
Nach Umformung:
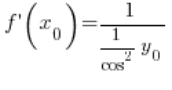
Mithilfe der trigonometrischen Identität können wir weiter umformen:
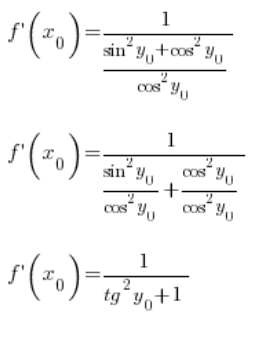
Achtung: ![]() ist der Wert der Funktion
ist der Wert der Funktion ![]() am Punkt
am Punkt 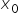 , also
, also 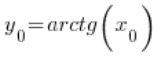 . Daher:
. Daher:
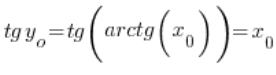 – da Tangens und Arkustangens Umkehrfunktionen sind, haben wir also:
– da Tangens und Arkustangens Umkehrfunktionen sind, haben wir also:
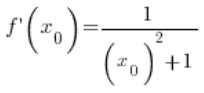 in jedem Punkt
in jedem Punkt ![]() (natürlich unter Berücksichtigung der Bedingungen des Definitionsbereichs, die ich vernachlässigt habe), somit wurde unsere Formel
(natürlich unter Berücksichtigung der Bedingungen des Definitionsbereichs, die ich vernachlässigt habe), somit wurde unsere Formel 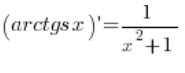 auf diese Weise nachgewiesen.
auf diese Weise nachgewiesen.
ENDE
Beim Schreiben dieses Beitrags habe ich mich auf Folgendes bezogen:
1. „Differential- und Integralrechnung. Band I.“ von G.M. Fichtenholz. Ausgabe 1966.
Klicke hier, um zur Hauptseite mit den Vorträgen über Ableitungen zurückzukehren

