Wzory na pochodne
Temat: Twierdzenie o pochodnej funkcji odwrotnej. Zastosowanie twierdzenia do wyprowadzenia kilku wzorów na pochodne.
Streszczenie
Na wykładzie zapoznamy się z twierdzeniem o pochodnej funkcji odwrotnej, udowodnimy je i zobaczymy, jak zastosować do wyznaczenia różnych wzorów na pochodne, wykazanie których bez tego twierdzenia (na przykład bezpośrednio z definicji, jak na poprzednim wykładzie) było by, ostrożnie pisząc – ciężkie.
Niestety przed zaatakowaniem twierdzenia wypadało by wiedzieć, co to jest funkcja odwrotna, dlaczego funkcją odwrotną do 
jest funkcja 
i dlaczego musimy się ograniczyć w tym przypadku do przedziału argumentów na przykład 
…
Wyprowadzanie wzorów przy pomocy twierdzenia o pochodnej funkcji odwrotnej jest dosyć częstym zadaniem z analizy matematycznej na studiach, także wykład może Ci się przydać w uczelnianych bojach.
Twierdzenie i dowód podaję korzystając z książki Fichtenholz’a, rozszerzając, zawężając, poprawiając literówki i przerabiając w paru punktach.
Twierdzenie o pochodnej funkcji odwrotnej
Jeżeli funkcja 
posiada funkcję odwrotną 
, oraz w punkcie 
ma skończoną i różną od zera pochodną 
, wtedy w odpowiadającym punkcie 
istnieje pochodna funkcji odwrotnej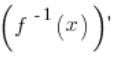 
i jej wartość w punkcie równa jest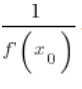 
.
Niezrozumiały ciąg znaczków? Na początku bardzo możliwe, że tak, wgryźmy się więc w to twierdzenie przy pomocy dwóch prostych, konkretnych przykładów.
Przykład 1
Jeżeli funkcja
posiada funkcję odwrotną
1. Weźmy funkcję 
w przedziale 
2. Funkcja odwrotna do niej istnieje równa jest 
– nie tłumaczę już dlaczego i po co te zastrzeżenie z przedziałem x, sorry…
oraz w punkcie
3. Weźmy punkt 
. Pochodna funkcji istnieje (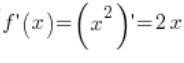
) i w punkcie jej wartość jest różna od zera (
).
wtedy w odpowiadającym
4. Odpowiadający punktowi punkt jest to odpowiadająca punktowi wartość funkcji , czyli 
.
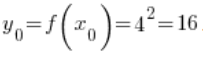Zatem w naszym przykładzie:
istnieje pochodna funkcji odwrotnej
5. Rzeczywiście, funkcja odwrotna jest , jej pochodna równa jest: 
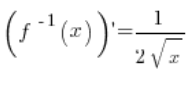(z podstawowych wzorów na pochodne) i w punkcie istnieje jak najbardziej i jest równa:
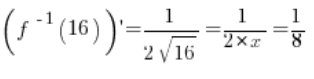
i jej wartość w punkcie
6. Rzeczywiście, obliczona w punkcie 5.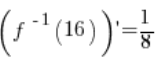 
jest równa:
(
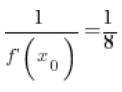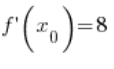– obliczyłem to w punkcie 3.)
Czyli Twierdzenie “działa” 🙂
Przykład 2
Jeżeli funkcja
1. Weźmy funkcję wykładniczą 
2. Funkcja odwrotna do niej istnieje równa jest 
– to było w średniej, nie tłumaczę również (funkcje logarytmiczna i wykładnicza to funkcje odwrotne)
oraz w punkcie
3. Weźmy punkt 
. Pochodna funkcji istnieje (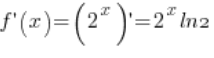
– podstawowe wzory na pochodne) i w punkcie jej wartość jest różna od zera (
).
wtedy w odpowiadającym
4. Odpowiadający punktowi punkt jest to wartość funkcji w punkcie , czyli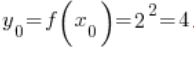 
.
Czyli:
istnieje pochodna funkcji odwrotnej
5. Rzeczywiście, funkcja odwrotna jest , jej pochodna równa jest: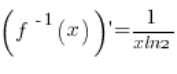 
(z podstawowych wzorów na pochodne). W punkcie pochodna istnieje i jest równa:
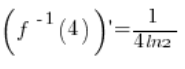
i jej wartość w punkcie
6. Rzeczywiście, obliczona w punkcie 5. 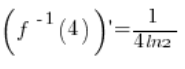jest równa:
(
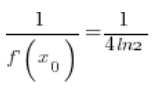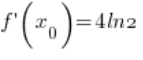– obliczyłem to w punkcie 3.)
Czyli Twierdzenie znowu “działa” 🙂
Dowód Twierdzenia o pochodnej funkcji odwrotnej
Udowodnimy to twierdzenie, odwołując się do interpretacji geometrycznej pochodnej funkcji w punkcie. Jak pamiętamy, wartość pochodnej funkcji w punkcie jest to tangens nachylenia stycznej do wykresu funkcji w tym punkcie.
Na wykresie wyglądało by to tak:
Wartość pochodnej w punkcie zdefiniowaliśmy na wcześniejszych wykładach jako tangens kąta 
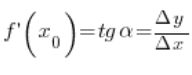
Zauważmy teraz ciekawą rzecz: wykres funkcji odwrotnej do można przedstawić na dokładnie tym samym wykresie, tylko, że należy pamiętać, iż czyta się go “na odwrót” – tzn. jakby argumentom y przyporządkowujemy wartości x (a więc przyrostem argumentów funkcji odwrotnej jest 
, a przyrostem odpowiadających jej wartości jest 
):
Zauważmy, że wartość pochodnej tej funkcji odwrotnej w punkcie równa jest:
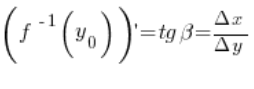
Widać więc, że wartość pochodnej z funkcji i wartość pochodnej jej funkcji odwrotnej to tangensy kątów w tym samym trójkącie prostokątnym.
A takie tangensy kątów w trójkącie prostokątnym (jak pamiętamy ze szkoły średniej) związane są zależnością:
Czyli (po obustronnym podzieleniu przez 
):
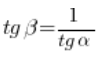
A z tego wynika wniosek naszego twierdzenia, czyli:
🙂
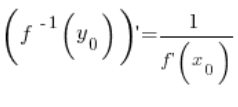
KONIEC DOWODU
Wyprowadzania wzorów na pochodne przy wykorzystaniu twierdzenia o pochodnej funkcji odwrotnej
Przykład 3
Wyprowadź wzór na pochodną funkcji 
.
Wzór, który mamy wyprowadzić, to: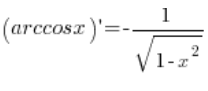 
.
Nasza funkcja f(x) jest to funkcja arccosx. Funkcja odwrotna do niej to funkcja 
. Pochodna z funkcji odwrotnej to 
.
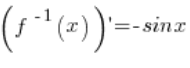Zgodnie z twierdzeniem o pochodnej funkcji odwrotnej wartość pochodnej z funkcji odwrotnej w punkcie równa jest odwrotności wartości pochodnej z funkcji w punkcie :
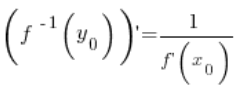
Czyli w dowolnym punkcie :
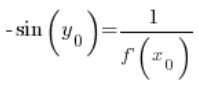
Po przekształceniu:
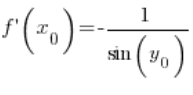
Korzystając z jedynki trygonometrycznej możemy wyprowadzić, że: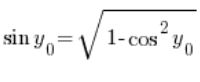 
, czyli mamy:
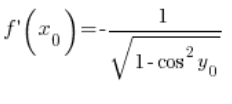
Teraz uwaga: jest to wartość funkcji w punkcie , czyli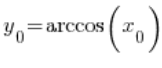 
. Zatem:
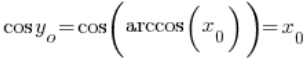– bo cosinus i arcus cosinus to funkcje odwrotne, mamy więc:
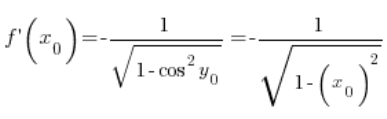w dowolnym punkcie (spełniającym oczywiście warunki z dziedziną, co zaniedbałem), zatem nasz wzór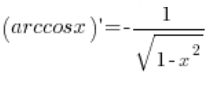 
został w ten sposób wykazany.
Przykład 4
Wyprowadź wzór na pochodną funkcji 
.
Wzór, który mamy wyprowadzić, to: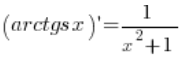 
.
Nasza funkcja f(x) jest to funkcja arctgx. Funkcja odwrotna do niej to funkcja 
. Pochodna z funkcji odwrotnej to 
.
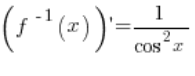Zgodnie z twierdzeniem o pochodnej funkcji odwrotnej wartość pochodnej z funkcji odwrotnej w punkcie równa jest odwrotności wartości pochodnej z funkcji w punkcie :
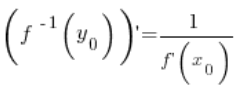
Czyli w dowolnym punkcie :
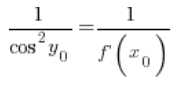
Po przekształceniu:
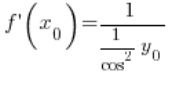
Korzystając z jedynki trygonometrycznej możemy przekształcić to dalej:
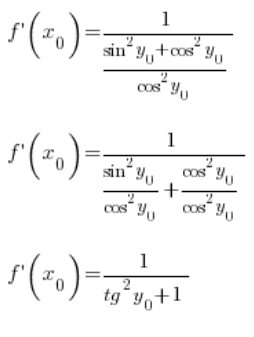
Teraz uwaga: jest to wartość funkcji w punkcie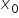 
, czyli 
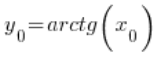. Zatem: 
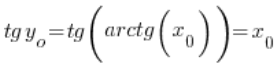– bo tangens i arcus tangens to funkcje odwrotne, mamy więc:
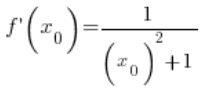w dowolnym punkcie (spełniającym oczywiście warunki z dziedziną, co zaniedbałem), zatem nasz wzór 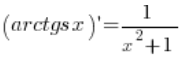został w ten sposób wykazany.
KONIEC
Pisząc tego posta korzystałem z…
1. “Rachunek różniczkowy i całkowy. Tom I.” G.M. Fichtenholz. Wyd. 1966.
Kliknij tutaj, aby zobaczyć, jak wykazać można własności pochodnych (następny Wykład) –>
Kliknij, aby powrócić na stronę główną z wykładami o pochodnych
A co z arcctg x ? Próbuje cały czas ale nie wychodzi /;
Wyprowadzenie wzoru na na pochodną funkcji f(x)=arcctg(x) będzie bardzo podobne to zamieszczonej w artykule pochodnej funkcji arctgx.
Wzór, który mamy wyprowadzić, to: \displaystyle \left( {arcctgx} \right)’=-\frac{1}{{{{x}^{2}}+1}}
Nasza funkcja f(x) jest to funkcja arcctgx. Funkcja odwrotna do niej to funkcja \displaystyle {{f}^{{-1}}}(x)=ctgx. Pochodna z funkcji odwrotnej to \displaystyle \left( {{{f}^{{-1}}}(x)} \right)’=\left( {ctg x} \right)’=-\frac{1}{{{{{sin }}^{2}}x}}(to wiem z podstawowych wzorów na pochodne).
Zgodnie z twierdzeniem o pochodnej funkcji odwrotnej wartość pochodnej z funkcji odwrotnej w punkcie \displaystyle {{y}_{0}}równa jest odwrotności wartości pochodnej z funkcji w punkcie \displaystyle {{x}_{0}}:
\displaystyle ({{f}^{{~-1}}}({{y}_{0}}))’=\frac{1}{{f'({{x}_{0}})}}
Czyli w dowolnym punkcie \displaystyle {{x}_{0}}:
\displaystyle -\frac{1}{{{{{sin }}^{2}}{{y}_{0}}}}=\frac{1}{{f'({{x}_{0}})}}
Po przekształceniu:
\displaystyle f'({{x}_{0}})=-{{sin }^{2}}{{y}_{0}}=-\frac{1}{{\frac{1}{{{{{sin }}^{2}}{{y}_{0}}}}}}
Korzystając z jedynki trygonometrycznej mogę przekształcić to dalej:
\displaystyle f'({{x}_{0}})=-\frac{1}{{\frac{{{{{sin }}^{2}}{{y}_{0}}+{{{cos }}^{2}}{{y}_{0}}}}{{{{{sin }}^{2}}{{y}_{0}}}}}}=-\frac{1}{{\frac{{{{{sin }}^{2}}{{y}_{0}}}}{{{{{sin }}^{2}}{{y}_{0}}}}+\frac{{{{{cos }}^{2}}{{y}_{0}}}}{{{{{sin }}^{2}}{{y}_{0}}}}}}=-\frac{1}{{1+{{{ctg }}^{2}}{{y}_{0}}}}
Wracając do pierwotnego rozwiązania:
\displaystyle {{y}_{0}}jest to wartość funkcji f(x)=arcctgx w punkcie \displaystyle {{x}_{0}}, czyli \displaystyle {{y}_{0}}=arcctg {{x}_{0}}.
Zatem: \displaystyle ctg {{y}_{0}}=ctg (arcctg ({{x}_{0}}))={{x}_{0}}– bo cotangens i arcus cotangens to funkcje odwrotne, mam więc:
\displaystyle f'({{x}_{0}})=-\frac{1}{{{{{({{x}_{0}})}}^{2}}+1}}w dowolnym punkcie \displaystyle {{x}_{0}}(spełniającym oczywiście warunki z dziedziną).
Zatem mam ostateczny wynik, zgadzający się z pierwotnym założeniem:
\displaystyle \left( {arcctg x} \right)’=-\frac{1}{{{{x}^{2}}+1}}
Zastanawiam się jak zrobić coś takiego: Dla funkcji dwóch zmiennych f(x,y) podać \interpretację równości fy'(5,3)=4. Wydaje mi się to banalnie proste, a z drugiej strony nie wiem jak się do tego zabrać. W miarę możliwości proszę o pomoc. Pozdrawiam.
Wykład był boski. Studenta 50+ nauczyłeś pochodnych funkcji odwrotnych. Pozdrawiam
Dzięki, pozdrawiam.
hmm a ja nadal nie rozumiem