Eulersche Substitutionen vom Typ I

---

Eulersche Substitutionen – wem nützen sie?

Eulersche Substitutionen in unbestimmten Integralen sind das nächste Thema, das nach rationalen Integralen, trigonometrischen Integralen und Wurzelintegralen (oder nach einigen Klassifizierungen: “irrationalen Integralen”) eingeführt wird. Das bedeutet, dass die meisten Studenten nicht das Vergnügen haben werden, sie zu treffen, und ich habe sie auch nicht in meinem Kurs für unbestimmte Integrale aufgenommen.

Es bleibt jedoch eine ziemlich große Gruppe von Studenten in mathematischen Studiengängen oder in wirklich, wirklich “starken” mathematischen Bereichen, die sich mit Eulerschen Substitutionen auseinandersetzen müssen, und diese (sowie Interessierte) lade ich ein. Ich werde alle drei Arten von Eulerschen Substitutionen besprechen (in diesem Beitrag werde ich die erste Art behandeln) und für jede einen Beispiel durchführen.

Lass uns starten.

Welche Integrale lösen wir mit Eulerschen Substitutionen?

Mit Eulerschen Substitutionen knacken wir Integrale des Typs:

…also irgendwelche willkürlichen Beziehungen zwischen und . Sie können also als eine Art “Erweiterung” des Themas Integrale mit Wurzeln (“irrationale Integrale”) betrachtet werden.

Mit Eulerschen Substitutionen knacken wir Integrale, die nicht einfacher gelöst werden können, natürlich. Zum Beispiel das Integral:

ist ein Integral, in dem wir eine Beziehung zwischen und haben, aber es kann sehr einfach durch eine dumme Substitution gelöst werden: . Also schießen wir nicht mit Kanonen auf Spatzen und quälen uns in solchen einfachen Integralen nicht mit Euler.

Nehmen wir jedoch das Integral:

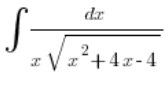
Wir sehen, dass die Situation ernster ist, die uns bisher bekannten Substitutionen , oder (wir können daraus nicht bestimmen) lösen das Problem nicht.

Wir brauchen eine neue Waffe.

Eulersche Substitutionen – erster Typ

Wenn wir ein Integral haben:

in dem ist,

wenden wir die Substitution an:

und quadrieren beide Seiten, die Terme kürzen sich heraus (und das ist der Punkt), wir bestimmen (in dieser Reihenfolge):

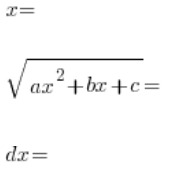
, ausgedrückt durch t, setzen wir in das ursprüngliche Integral ein:

und wir erhalten ein Integral in Bezug auf t (wenn wir darin noch x’s haben, haben wir einen Fehler gemacht) und es ist ein rationales Integral.

Hinweis

Es ist noch hinzuzufügen, dass in der Praxis viele Studenten nur Eulersche Substitutionen des ersten Typs kennen und nur für Integrale des Typs:

, also solche, in denen quasi

Lassen Sie uns Eulersche Substitutionen des ersten Typs in Aktion verfolgen, zum Beispiel:

Beispiel 1

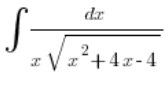
Wir stellen fest, dass es sich um ein Integral handelt, in dem es eine Beziehung zwischen und gibt. Dass es nicht einfach zu lösen ist. Dass ( ist natürlich der Koeffizient neben , in unserem Beispiel ist es 1).

Also werden wir Eulersche Substitutionen des ersten Typs anwenden.

Ich setze ein:

das heißt einfach:

ich quadriere beide Seiten:

Die Terme mit auf beiden Seiten kürzen sich heraus (und das ist immer der Fall):

Und jetzt müssen wir , und bestimmen (in dieser Reihenfolge).

Wir beginnen mit :

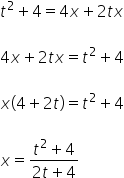
Wir haben ausgedrückt durch die Variable t. Jetzt ist an der Reihe, also in unserem Beispiel: .

Wir kehren zu unserer ersten Substitution zurück, bei der es war:

Jetzt kennen wir bereits (man sieht, warum die Reihenfolge wichtig ist, oder?), also können wir schreiben:

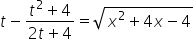
das heißt:

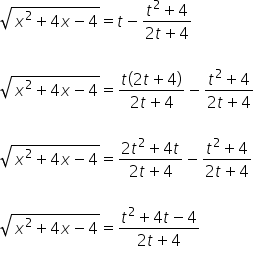
So haben wir ausgedrückt durch die Variable .

Zuletzt nehmen wir , das wir einfach durch Differenzieren beider Seiten des bestimmten erhalten:

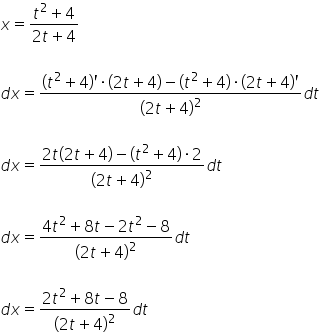
Und so bestimmen wir . Wir haben also:

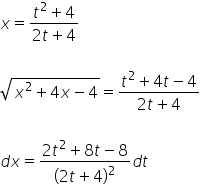
Wir setzen das alles in das ursprüngliche Integral ein:

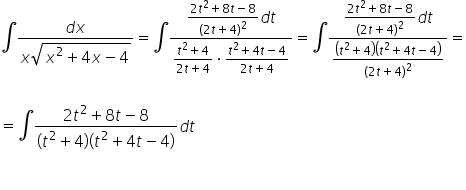
Auf den ersten Blick sieht es wie ein langweiliges, mühsames, aber bereits bekanntes und schematisches rationales Integral aus (Zerlegung in Partialbrüche, der zweite Faktor im Nenner kann noch weiter zerlegt werden). In der Regel ist das so, aber in diesem speziellen Beispiel werden wir etwas Glück haben und uns das Durchkämpfen durch 3 Seiten A4 Berechnungen ersparen:

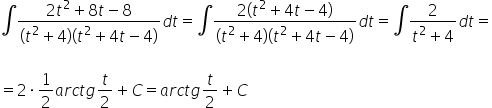
Wie kehren wir zur Substitution zurück? Wir hatten am Anfang:

Daraus folgt natürlich:

Unser Ergebnis ist also:

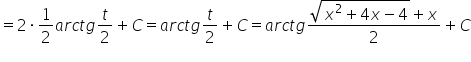
Fortsetzung folgt. (Wir haben noch zwei weitere Arten von Eulerschen Substitutionen, was ist, wenn der Koeffizient nicht größer als null ist?)