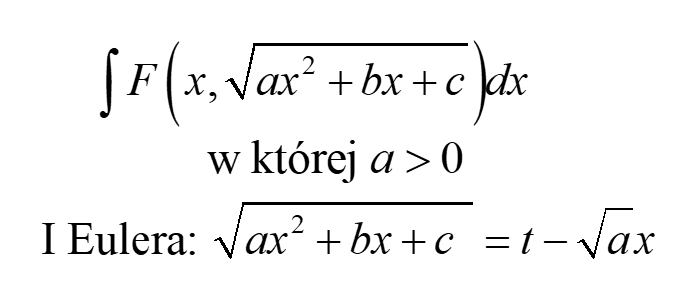
Euler Substitutions of the First Kind

---

Euler Substitutions – Who Needs Them?

Euler substitutions in indefinite integrals are the next topic introduced after rational integrals, trigonometric integrals, and integrals with roots (or according to some classifications: “irrational integrals”). This means that most students won’t have the pleasure of encountering them. I also didn’t include them in my Course on Indefinite Integrals.

However, there remains a quite significant group of students in mathematical disciplines, or those really, really “strong” in mathematics, who have to tackle Euler substitutions, and I invite those (as well as the curious ones). I will discuss all three types of Euler substitutions (in this post, I’ll tackle the first kind) and make one example for each.

Let’s go.

What Kind of Integrals Do We Solve with Euler Substitutions?

Euler substitutions help us crack integrals of the type:

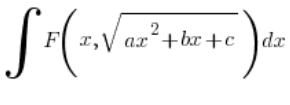
…so, any random relations between and . They can be seen as a sort of “extension” of the topic of integrals with roots (“irrational”).

We use Euler substitutions for integrals that can’t be solved more simply, of course. For example, the integral:

is an example of an integral with the relation and , but it can be solved very simply by a straightforward substitution: . So we don’t need to use a cannon to kill a sparrow and for such simple integrals, we don’t bother with Euler.

But let’s consider the integral:

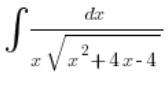
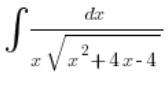
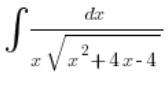
We see the situation is more serious, and our previously known substitutions , or (we can’t express from them) won’t solve it.

We need a new weapon.

Euler Substitutions – Type I

Given an integral:

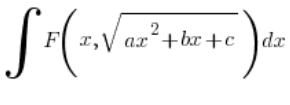
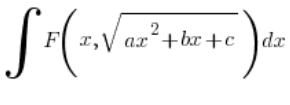
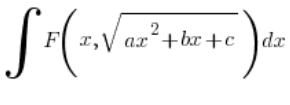
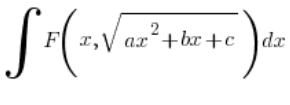
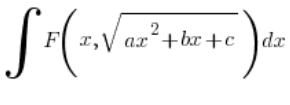
where ,

we apply the substitution:

Raise both sides to the square, the terms cancel out (and that’s the point), and we determine (in order):

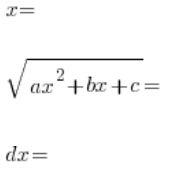
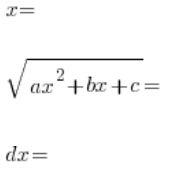
expressed with relations of t, and substitute into the original integral:

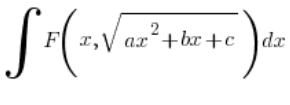
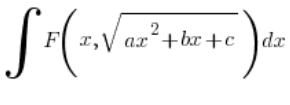
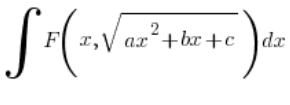
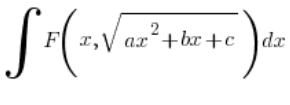
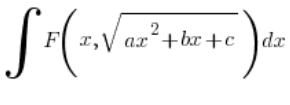
and we end up with an integral in terms of t (if we still have any x’s left, we’ve made a mistake), and it is a rational integral.

Note

It’s also worth adding that in practice, many students are only introduced to Euler’s substitutions of Type I, and only for integrals of the type:

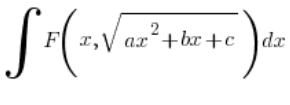
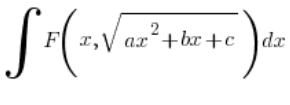
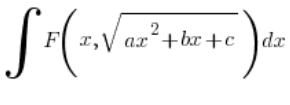
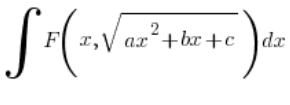
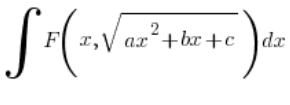
, i.e., those where it appears as if

Let’s follow the Euler substitutions of the first kind in action, using this example:

Example 1

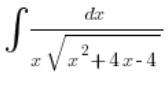
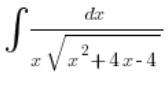
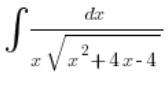
We determine that this is an integral where the relationship between and exists. It cannot be solved simply. We notice that ( is of course the coefficient at , in our example it is equal to 1).

So, we will be using the Euler substitution of the first kind.

I substitute:

which simply means:

I raise both sides to the square:

The terms with on both sides cancel each other out (and that’s how it’s supposed to be each time):

And now, we need to determine , and (in that order).

Let’s start with :

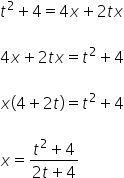
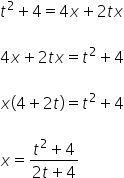
We have expressed in terms of t. Now it’s time for , which in our case is: .

We go back to our first substitution, which was:

Now that we know (you see why the order is important, right?), we can write:

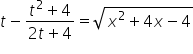
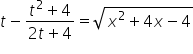
which means:

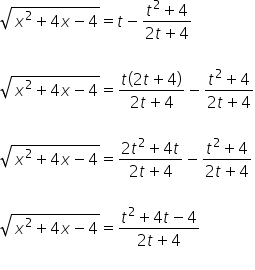
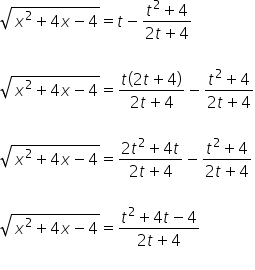
So, we have expressed by the variable .

Finally, , which we simply get by differentiating both sides of the determined :

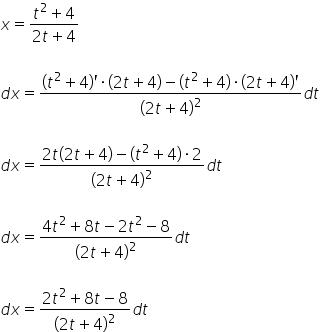
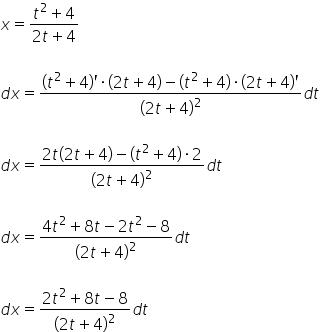
And that’s how we determine . So, we have:

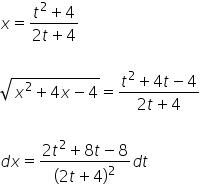
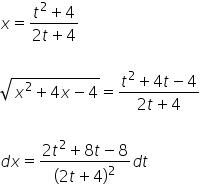
We substitute all of this into the original integral:

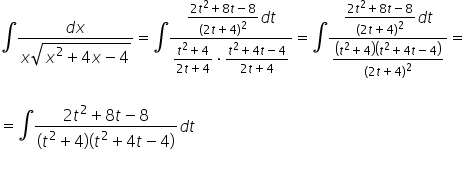
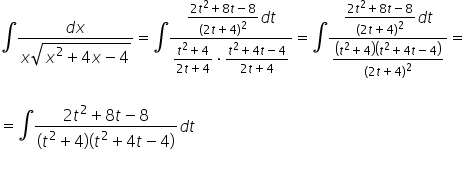
At first glance, this looks like a tedious, yet familiar rational integral (decomposition into partial fractions, the second factor in the denominator can be further decomposed). Usually, that’s the case, but in this specific example, we’ll be a bit lucky and avoid going through 3 pages of A4 calculations:

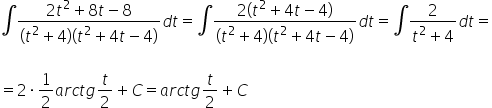
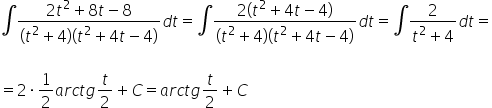
How to return to the substitution? Initially, we had:

From which, of course:

Thus, our result is:

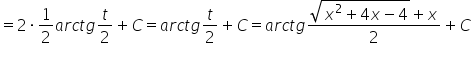
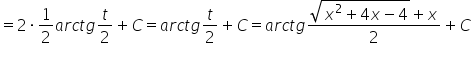
To be continued. (we still have two more types of Euler substitutions to cover, what if the coefficient is not greater than zero?).