Bei schwierigeren Aufgaben zu bestimmten Integralen ist es oft gut, wachsam zu bleiben – eine scheinbar sehr schwierige Aufgabe kann mit einer einfachen Formel aus der Mittelschule gelöst werden.
Aufgabe zum Volumen eines Rotationskörpers
Nehmen wir an, wir müssen das Volumen eines Körpers berechnen, der durch Drehen einer Kurve entsteht:
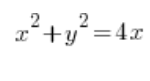
sich um die OX-Achse dreht (na gut, sagen wir „rotiert“). Ein paar geordnete Bewegungen, bekannt aus der Oberschule…
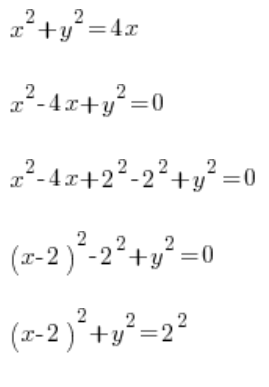
…und wir stellen fest, dass unsere Kurve einfach ein kleines Kreis mit dem Zentrum im Punkt (2,0) und einem Radius von 2 ist. Was nun? Wir leiten y aus der Formel ab und treiben das bestimmte Integral voran: 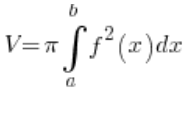 ?
?
Lösung
Nein… halten wir mal kurz inne. Atmen wir tief ein. Überlegen wir. Ein kleiner Kreis… Er dreht sich… Was entsteht durch solch eine Drehung? Natürlich eine Kugel. Die Formel für das Volumen einer Kugel kennen wir aus der Mittelschule:
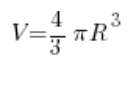
Den Radius kennen wir bereits (er beträgt zwei), das bedeutet:
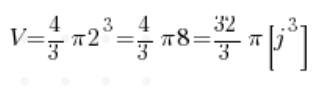
Und voilà, wir haben die Antwort, ohne auch nur die Integrale anzurühren 🙂


