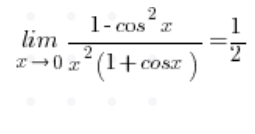Nützliche Grenze einer Funktion mit Kosinus
Krystian Karczyński
Gründer und Chef des Dienstes eTrapez.
Master of Mathematics der Technischen Universität Pozen (Polen). Mathematik-Nachhilfelehrer mit langjähriger Erfahrung. Schöpfer der ersten eTrapez-Kurse, die bei Studenten in ganz Polen große Beliebtheit erlangten.
Lebt in Stettin (Polen). Mag Waldspaziergänge, Strandtage und Kajakfahren.
Grenzwerte von Funktionen mit Sinus behandeln wir normalerweise mit der Formel: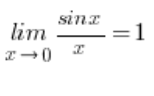 
(die Herleitung dieser Formel findest du hier). Ich zeige diese Methode auch in meinem Grenzwerte-Kurs.
Frage: Was ist mit Cosinus x?
Formel für den Grenzwert einer Funktion mit Cosinus
Natürlich gilt nicht: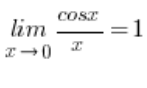 
, weil der Grenzwert der Funktion 
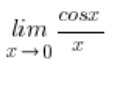überhaupt keine unbestimmte Form ist.
Für Grenzwerte mit Cosinus x ist die folgende Formel oft hilfreich:
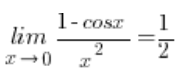– in vielen Lehrbüchern wird diese Formel “von Anfang an” ohne Beweis angegeben, während in vielen anderen sie als Grenzwert einer Funktion dargestellt wird, der erst berechnet werden muss.
Egal wie es in deinem Fall ist, es ist wert zu wissen, wie man diese Formel herleitet, und es geht so:
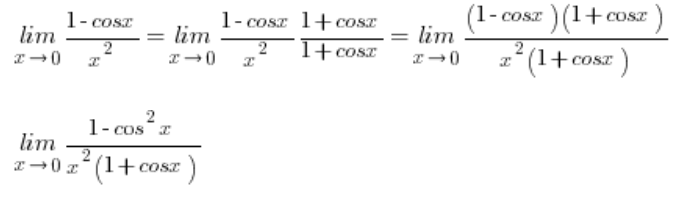
An dieser Stelle verwende ich die trigonometrische Identität im Zähler:
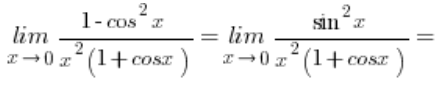
Der Grenzwert der Funktion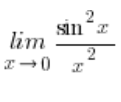 
konvergiert zu 
, weil:
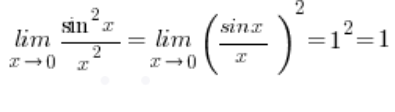
Und der Grenzwert der Funktion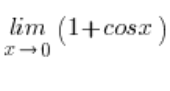 
konvergiert zu 
, weil 
, so dass wir das Ergebnis haben:
Suchen Sie nach Mathe-Nachhilfe für das Universitätsniveau oder die Oberstufe? Oder benötigen Sie vielleicht einen Kurs, der Sie auf das Abitur vorbereitet?
Wir sind das Team von eTrapez. Wir unterrichten Mathematik auf eine klare, einfache und sehr detaillierte Weise - wir erreichen sogar diejenigen, die sich am meisten gegen das Lernen sträuben.
Wir haben Kurse in Videoform erstellt, die in einer verständlichen Sprache erklärt sind, zum Herunterladen auf Computer, Tablet oder Handy. Sie starten die Aufnahme, schauen und hören zu, als wären Sie bei der Nachhilfe. Zu jeder Tages- und Nachtzeit.
