Currently Empty: zł0.00
Krystian Karczyński- 21 junio 2024
- Comment 0
Normalmente tratamos los problemas de límites de funciones con seno utilizando la fórmula: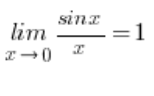 
(puedes encontrar la derivación de esta fórmula aquí). También muestro este método en mi Curso de Límites.
Pregunta: ¿qué pasa con el coseno x?
Fórmula para el límite de una función con coseno
Obviamente, no tenemos: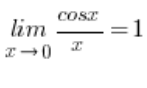 
, porque el límite de la función 
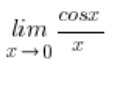no es una forma indeterminada en absoluto.
Para límites con coseno x, la siguiente fórmula es a menudo útil:
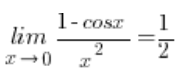– en muchos libros de texto, esta fórmula se da «desde el principio» sin demostración, mientras que en muchos otros se presenta como un límite de una función que necesita ser calculado.
Independientemente de tu situación, vale la pena conocer la derivación de esta fórmula, y va así:
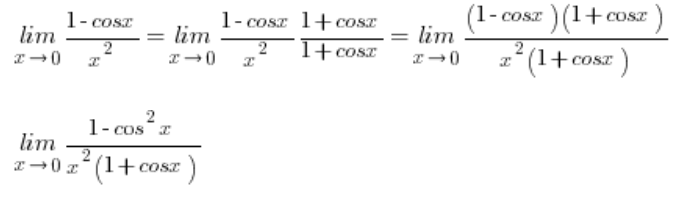
En este punto, utilizo la identidad trigonométrica en el numerador:
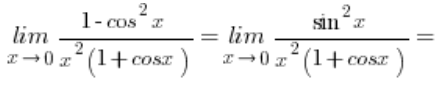
El límite de la función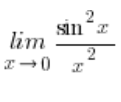 
converge a 
, porque:
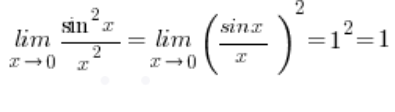
Y el límite de la función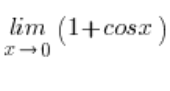 
converge a 
, porque 
, así que tenemos el resultado:
