Es befinden sich momentan keine Produkte im Warenkorb.
Krystian Karczyński- 24 Juni 2024
- Komentarz 0
Schwierigere Grenzwerte von Funktionen erfordern oft eine Substitution, zum Beispiel:
Beispiel
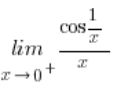
Der Grenzwert im Zähler existiert nicht, im Nenner nähert er sich null… Wohin strebt das Ganze?
Eine geeignete Substitution wäre: 
Aus der Substitution folgt, dass: 
Und dass, wenn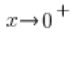 
, dann 
. Also haben wir:
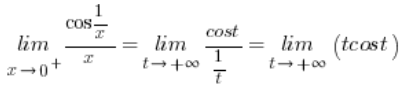
Und dieser Grenzwert existiert nicht, was in der Weise gezeigt werden kann, wie in einem anderen meiner Beiträge gezeigt wird.
