استنتاج صيغ للمشتقات
صيغ المشتقات لم تأت من الفضاء، بل هي في الواقع مستنتجة من تعريف المشتقة:
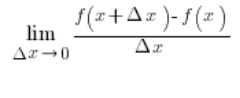
مشتقة جذر x التربيعي
لنستنتج على سبيل المثال صيغة لمشتقة جذر x التربيعي: ![]() . يجب أن نحصل على:
. يجب أن نحصل على: ![]() (كما تقول الصيغ الأساسية للمشتقات – الصيغة رقم 5).
(كما تقول الصيغ الأساسية للمشتقات – الصيغة رقم 5).
لدينا 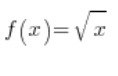 . هيا بنا. بعد التعويض في صيغة المشتقة من التعريف، سنحصل على:
. هيا بنا. بعد التعويض في صيغة المشتقة من التعريف، سنحصل على:
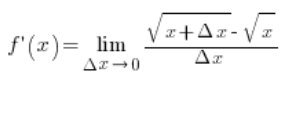
من خلال ضرب البسط والمقام بالطريقة التالية…
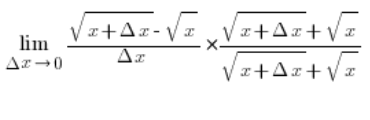
…واستخدام صيغة المربع الكامل في البسط، سنقضي على اللاعقلانية وسننتهي بهذا:
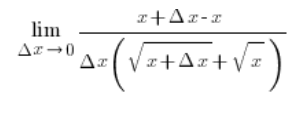
المتغيرات x في أعلى البسط ستُلغى ونحصل…
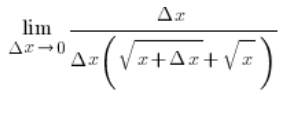
…وبعد إلغاء ![]() في البسط والمقام:
في البسط والمقام:
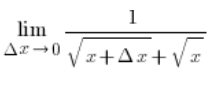
بما أن ![]() فهذا يعني:
فهذا يعني:
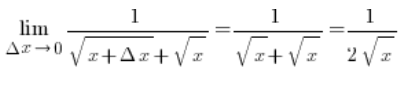
إذاً، لقد وصلنا إلى البيت. تم استنتاج صيغة المشتقة.
المزيد من الأمثلة
يمكنك التجربة بصيغ أخرى، أشجعك على ذلك!
دورة المشتقات وتحليل سلوك الدالة
يمكنك أيضًا العثور على حالات محسوبة خطوة بخطوة في دورتي للمشتقات وتحليل سلوك الدالة.
الحالات الأكثر عمومية
مهمة استنتاج صيغة لمشتقة ترجع دائمًا إلى حساب الحد المناسب، حيث يتم التعامل مع ‘x’ كثابت. قد تكون أسهل أو أصعب، لكن يمكنك استخدام الطرق والحيل التي تعرفها بالفعل من حساب حدود الدالة.
مع ملاحظة واحدة.
للأسف – تقع قاعدة لوبيتال خارج الاعتبار. لماذا؟ بالضبط لأنها تستخدم المشتقات.
دعني أذكرك بمهمتك – عليك أن تحسب مشتقة الدالة من التعريف، دون معرفة الصيغة. وتستخدم قاعدة لوبيتال غالبًا صيغ المشتقات!


