
Pochodna z pierwiastka x – jak wyprowadzić wzór
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Wyprowadzanie wzorów na pochodne funkcji
Wzory na pochodne nie wzięły się z kosmosu, tylko po prostu są one wyprowadzone z definicji pochodnej:
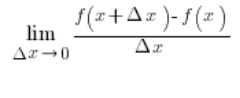
Pochodna z pierwiastka x
Wyprowadźmy na przykład wzór na pochodną pierwiastka z x: ![]() . Powinniśmy otrzymać wynik:
. Powinniśmy otrzymać wynik: ![]() (tako rzeczą podstawowe wzory na pochodne – wzorek numer 5).
(tako rzeczą podstawowe wzory na pochodne – wzorek numer 5).
Mamy 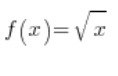 . Do dzieła. Po podstawieniu do wzoru na pochodną z definicji otrzymamy:
. Do dzieła. Po podstawieniu do wzoru na pochodną z definicji otrzymamy:
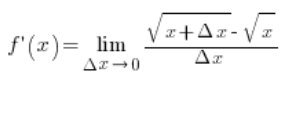
Mnożąc licznik i mianownik w następujący sposób…
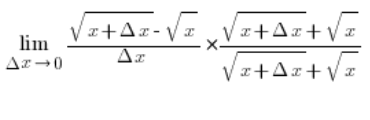
…i korzystając ze wzoru skróconego mnożenia w liczniku pozbędziemy się w nim niewymierności i wyjdziemy na:
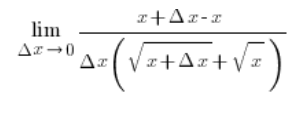
x-sy na górze w liczniku się skrócą i otrzymamy…
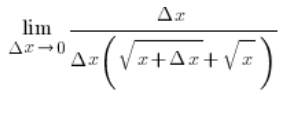
…a po skróceniu ![]() w liczniku i mianowniku:
w liczniku i mianowniku:
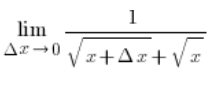
Skoro ![]() oznacza to, że:
oznacza to, że:
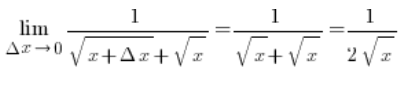
Czyli jesteśmy w domu. Wzór na pochodną wyprowadzony.
Więcej przykładów
Możesz pokombinować z innymi wzorami, zachęcam!
Kurs Pochodne i Badanie Przebiegu Zmienności Funkcji
Różne przypadki obliczone krok po kroku znajdziesz również w moim Kursie Pochodne i Badanie Przebiegu Zmienności Funkcji.
Przypadki bardziej ogólne
Zadanie na wyprowadzenie wzoru na pochodną sprowadzi się zawsze do obliczenia odpowiedniej granicy, w której 'x’ traktujesz jak stałą. Może być ono łatwiejsze, lub trudniejsze, ale możesz stosować w nim metody i sztuczki znane już Tobie z liczenia granic funkcji.
Może z jednym zastrzeżeniem.
Niestety – odpada reguła de l’Hospitala. Dlaczego? No właśnie dlatego, że wykorzystuje się w niej pochodne.
Przypomnę Ci Twoje zadanie – musisz policzyć pochodną funkcji z definicji, bez znajomości wzoru. A regule de l’Hospitala wykorzystuje się właśnie wzory na pochodne i to często!
Bestsellery

Kurs Statystyka
Studia / Autor: mgr Krystian Karczyński
Pierwotna cena wynosiła: 49,00 zł.34,30 złAktualna cena wynosi: 34,30 zł.

Kurs Macierze
Studia / Autor: mgr Krystian Karczyński
Pierwotna cena wynosiła: 49,00 zł.34,30 złAktualna cena wynosi: 34,30 zł.

Kurs Równania Różniczkowe
Studia / Autor: mgr Krystian Karczyński
Pierwotna cena wynosiła: 49,00 zł.34,30 złAktualna cena wynosi: 34,30 zł.

Kurs Wytrzymałość Materiałów
Studia / Autor: mgr inż. Adam Kasprzak
Pierwotna cena wynosiła: 49,00 zł.34,30 złAktualna cena wynosi: 34,30 zł.
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.





Ile to bedzie pierwiastek 3 stopnia z x^3+y^2 po dwóch zmiennych i jeszcze podwojna pochodna?
Pochodne drugiego rzędu:
Witam! Czy mógłby mi Pan (lub ktokolwiek kto wie jak to zrobić) pomóc z wyznaczeniem pochodnej funkcji z definicji? Chodzi mi o ogólną pochodną nie w punkcie.
Chodzi mi o ogólną pochodną nie w punkcie.
Witam! Czy byłaby możliwość, aby obliczył Pan pochodną z definicji dla jakiejkolwiek funkcji cyklometrycznej ? Pozdrawiam
Witam! Czy byłaby możliwość, aby obliczył Pan pochodną z definicji: (arcsinx)’ ? Pozdrawiam
jak obliczyć pochodną y=pierwiastek z x a x0=4?
Jak obliczyć pochodną x+1/ pierwiastek z 1-x ?
By policzyć pochodną takiej funkcji \displaystyle y=\frac{{x+1}}{{\sqrt{{1-x}}}}
wykorzystuję wzór na pochodną ilorazu dwóch funkcji, czyli:
\displaystyle \left( {\frac{f}{g}} \right)’=\frac{{f’\cdot g-f\cdot g’}}{{{{g}^{2}}}}
Stąd otrzymujemy:
\displaystyle y’=\left( {\frac{{x+1}}{{\sqrt{{1-x}}}}} \right)’=\frac{{\left( {x+1} \right)’\cdot \left( {\sqrt{{1-x}}} \right)-\left( {x+1} \right)\cdot \left( {\sqrt{{1-x}}} \right)’}}{{{{{\left( {\sqrt{{1-x}}} \right)}}^{2}}}}=
Wykorzystuję wzór na pochodną pierwiastka, z tym, że pod pierwiastkiem jest „coś więcej niż sam x” (tutaj oznaczyłam to trójkącikiem), dlatego muszę pamiętać o przemnożeniu razy pochodna tego wyrażenia „coś więcej”, tego czegoś w środku.
Mam więc jakby: \displaystyle \left( {\sqrt{\Delta }} \right)’=\frac{1}{{2\sqrt{\Delta }}}\cdot \Delta ’
No to wracamy do obliczeń pochodnej:
\displaystyle =\frac{{\left( {1+0} \right)\cdot \sqrt{{1-x}}-\left( {x+1} \right)\cdot \frac{1}{{2\sqrt{{1-x}}}}\cdot \left( {1-x} \right)’}}{{{{{\left( {\sqrt{{1-x}}} \right)}}^{2}}}}=\frac{{\sqrt{{1-x}}-\frac{{x+1}}{{2\sqrt{{1-x}}}}\cdot \left( {0-1} \right)}}{{1-x}}=
\displaystyle =\frac{{\frac{{2\sqrt{{1-x}}}}{{2\sqrt{{1-x}}}}\sqrt{{1-x}}+\frac{{x+1}}{{2\sqrt{{1-x}}}}}}{{1-x}}=\frac{{\frac{{2{{{\left( {\sqrt{{1-x}}} \right)}}^{2}}}}{{2\sqrt{{1-x}}}}+\frac{{x+1}}{{2\sqrt{{1-x}}}}}}{{1-x}}=\frac{{\frac{{2\left( {1-x} \right)+x+1}}{{2\sqrt{{1-x}}}}}}{{1-x}}=
\displaystyle =\frac{{\frac{{2-2x+x+1}}{{2\sqrt{{1-x}}}}}}{{1-x}}=\frac{{3-x}}{{2{{{\left( {1-x} \right)}}^{{\frac{1}{2}}}}}}\cdot \frac{1}{{{{{\left( {1-x} \right)}}^{1}}}}=\frac{{3-x}}{{2{{{\left( {1-x} \right)}}^{{\frac{3}{2}}}}}}
jak obliczyć pochodną : pierwiastek 3-go stopnia z x+1 ?
Zamienić na potęgę i potem już z górki:
{{\left( {{\left( x+1 \right)}^{\frac{1}{3}}} \right)}^{\prime }}=\frac{1}{3}{{\left( x+1 \right)}^{-\frac{2}{3}}}{{\left( x+1 \right)}^{\prime }}=\frac{1}{3}{{\left( x+1 \right)}^{-\frac{2}{3}}}=\frac{1}{3}\frac{1}{{{\left( x+1 \right)}^{\frac{2}{3}}}}
Jak wygląda pochodna po v z Z=u^pierwiastek z v
wiem, że na pewno będzie to u ^pierwiastek z v * ln u ale dlaczego mam, że tam jest jeszcze to podzielone przez 2\pierwiastki z v??
A pochodna funkcji y=(8-2x)^1/2 w punkcie x(0)=-5 ?
Witam!
Dziękuję za powyższe przykłady. A jak można wyprowadzić pochodną a do potęgi x?
A co z taką funkcją:
U(x,y) = [X(1+Y)]^1/2
Gubię się w wyprowadzaniu pochodnych z tego, co pod pierwiastkiem 🙁
Będzie tak:
\frac{\partial U}{\partial X}={{\left( \sqrt{X\left( 1+Y \right)} \right)}^{\prime }}=\frac{1}{2\sqrt{X\left( 1+Y \right)}}{{\left( X\left( 1+Y \right) \right)}^{\prime }}=\frac{1}{2\sqrt{X\left( 1+Y \right)}}\left( 1+Y \right)=\frac{1+Y}{2\sqrt{X\left( 1+Y \right)}}
\frac{\partial U}{\partial Y}={{\left( \sqrt{X\left( 1+Y \right)} \right)}^{\prime }}=\frac{1}{2\sqrt{X\left( 1+Y \right)}}{{\left( X\left( 1+Y \right) \right)}^{\prime }}=\frac{1}{2\sqrt{X\left( 1+Y \right)}}\cdot X=\frac{X}{2\sqrt{X\left( 1+Y \right)}}
Jak liczymy pochodną po X, traktujemy Y jak stałą, liczbę. Można nawet sobie wyobrazić, że w miejscu Y stoi jakaś konkretna liczba, np. 5.
Jak liczymy po Y, wtedy odwrotnie, traktujemy X jak stałą 🙂
Witam!
Jak obliczać pochodne po x i po y z funkcji użyteczności, która ma postać U(x,y)= (X^2 + Y^2)^1/2?
Witam:
Pochodną po X:
\frac{\partial U}{\partial X}={{\left( \sqrt{{{X}^{2}}+{{Y}^{2}}} \right)}^{\prime }}=\frac{1}{2\sqrt{{{X}^{2}}+{{Y}^{2}}}}{{\left( {{X}^{2}}+{{Y}^{2}} \right)}^{\prime }}=\frac{1}{2\sqrt{{{X}^{2}}+{{Y}^{2}}}}\cdot 2X=\frac{X}{\sqrt{{{X}^{2}}+{{Y}^{2}}}}
Pochodną po Y:
\frac{\partial U}{\partial Y}={{\left( \sqrt{{{X}^{2}}+{{Y}^{2}}} \right)}^{\prime }}=\frac{1}{2\sqrt{{{X}^{2}}+{{Y}^{2}}}}{{\left( {{X}^{2}}+{{Y}^{2}} \right)}^{\prime }}=\frac{1}{2\sqrt{{{X}^{2}}+{{Y}^{2}}}}\cdot 2Y=\frac{Y}{\sqrt{{{X}^{2}}+{{Y}^{2}}}}
Czyli po prostu tak samo, jak wszystkie pochodne funkcji dwóch zmiennych.
Mam problem jak policzyć pochodną z pierwiastek 7 stopnia z x oraz pierwiastek 3 stopnia z x do 4 bo nie pamiętam jak to się robiło a niestety zginęły mi notatki 😉
1. Pochodna z pierwiastka 7 stopnia z x Z DEFINICJI?
Bo z gotowego wzoru to sprawa jest łatwa:
{{\left( {{x}^{\frac{1}{7}}} \right)}^{\prime }}=\frac{1}{7}{{x}^{\frac{1}{7}-1}}=\frac{1}{7}{{x}^{-\frac{6}{7}}}=\frac{1}{7}\frac{1}{{{x}^{\frac{6}{7}}}}
Jeśli jednak na pewno na 100% z definicji to wykazał bym tą pochodną z pierwiastka tak:
\underset{\Delta x\to 0}{\mathop{lim }}{{x}^{-\frac{6}{7}}}\frac{{{\left( 1+\tfrac{\Delta x}{x} \right)}^{\frac{1}{7}}}-1}{\frac{\Delta x}{x}}
Tu skorzystał bym z pewnego mniej znanego wzoru na granicę (jak trzeba, to musiał bym jeszcze go wyprowadzić): \underset{\square to 0}{\mathop{lim }}\frac{{{\left( 1+square \right)}^{n}}-1}{\square }=n
No i mam:
\underset{\Delta x\to 0}{\mathop{lim }}{{x}^{-\frac{6}{7}}}\frac{{{\left( 1+\tfrac{\Delta x}{x} \right)}^{\frac{1}{7}}}-1}{\frac{\Delta x}{x}}={{x}^{-\frac{6}{7}}}\cdot \frac{1}{7}=\frac{1}{7}{{x}^{-\frac{6}{7}}}
Warto zauważyć, że tą metodę można zastosować do wyprowadzania wzoru na pochodną z pierwiastka dowolnego stopnia, a nawet do najbardziej ogólnego wzoru: {{\left( {{x}^{n}} \right)}^{\prime }}=n{{x}^{n-1}}dla dowolnych nrzeczywistych!
2. Można jak wyżej, zamieniając pierwiastek trzeciego stopnia na potęgę {{x}^{\frac{4}{3}}}.
ile wynosi pochodna z x / pierwiastek z 5 ???
Rozumiem, że chodzi o taką pochodną:
\left( \frac{x}{sqrt{5}} \right) \prime ?
Najlepiej obliczyć ją tak:
\left( \frac{x}{sqrt{5}} \right) \prime=\left(\frac{1}{sqrt{5}}x\right)\prime=\frac{1}{sqrt{5}}\left(x\right)\prime=\frac{1}{sqrt{5}}
Czyli można tu zastosowac uogólnienie, że jeżeli pod pierwiastkiem nie ma x wtedy pierwiastek po prostu przepisujemy, a tworzymy pochodną tylko od x, np x*pierwiastek z jakiś dowolnych a*b bedzie wynosić w tym przypadku właśnie niezmieniony pierwiastek z a i b?