Формули для похідних
Тема: Теорема про похідну оберненої функції. Застосування теореми для виведення декількох формул похідних.
Резюме
На нашій лекції ми зануримося в цю круту теорему про похідну оберненої функції. Ми її доведемо і побачимо, як використовувати її для визначення цілого ряду формул похідних. Без цієї теореми виведення цих формул (як ми робили це безпосередньо з визначень на попередній лекції) було б, м’яко кажучи, складним.
Перш ніж братися за теорему, було б чудово знати, що таке обернена функція, чому оберненою до ![]() є функція
є функція ![]() і чому ми повинні обмежити себе в цьому випадку до інтервалу аргументів, наприклад,
і чому ми повинні обмежити себе в цьому випадку до інтервалу аргументів, наприклад, ![]() …
…
Виведення формул за допомогою теореми про похідну оберненої функції є досить частим завданням з математичного аналізу на рівні університету, тому ця лекція може стати в нагоді в університетських битвах.
Теорему та доказ я взяв з книги Фіхтенгольца, розширив, скоротив, виправив помилки та переробив у декількох місцях.
Теорема про похідну оберненої функції
Якщо функція ![]() має обернену функцію
має обернену функцію ![]() , та в точці
, та в точці ![]() має скінченну і відмінну від нуля похідну
має скінченну і відмінну від нуля похідну ![]() , то в відповідній точці
, то в відповідній точці ![]() існує похідна оберненої функції
існує похідна оберненої функції 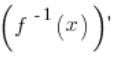 і її значення в точці
і її значення в точці ![]() дорівнює
дорівнює 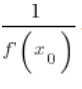 .
.
Заплуталися в цьому ланцюжку символів? Спочатку це дуже ймовірно, але давайте глибше зануримося в цю теорему за допомогою кількох простих, конкретних прикладів.
Приклад 1
Якщо функція
має обернену функцію
,
1. Візьмемо функцію ![]() в інтервалі
в інтервалі ![]()
2. Обернена функція до неї існує та дорівнює ![]() – я не пояснюю чому та навіщо це обмеження в інтервалі x, вибачте…
– я не пояснюю чому та навіщо це обмеження в інтервалі x, вибачте…
та в точці
має скінченну та відмінну від нуля похідну
,
3. Візьмемо точку ![]() . Похідна функції
. Похідна функції ![]() існує (
існує (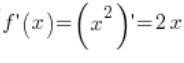 ) та в точці
) та в точці ![]() її значення відрізняється від нуля (
її значення відрізняється від нуля (![]() ).
).
тоді у відповідній точці
точка
4. Відповідна точці ![]() точка
точка ![]() є значенням функції
є значенням функції ![]() у точці
у точці ![]() , тобто
, тобто 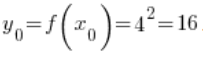 .
.
Отже, в нашому прикладі:
![]()
існує похідна оберненої функції
5. Дійсно, обернена функція є ![]() , її похідна дорівнює:
, її похідна дорівнює: 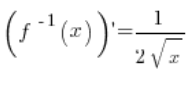 (за основними формулами похідних) і в точці
(за основними формулами похідних) і в точці ![]() вона існує і дорівнює:
вона існує і дорівнює:
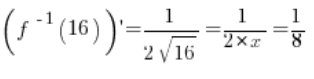
і її значення в точці
дорівнює
.
6. Дійсно, розраховане в пункті 5. 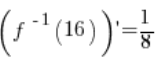 дорівнює:
дорівнює:
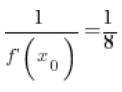 (
(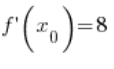 – я розрахував це в пункті 3.)
– я розрахував це в пункті 3.)
Отже, Теорема “працює” 🙂
Приклад 2
Якщо функція
має обернену функцію
,
1. Візьмемо експоненціальну функцію ![]()
2. Обернена до неї функція існує і дорівнює ![]() – це було у середній школі, тому не буду знову пояснювати (логарифмічна та експоненціальна функції є оберненими)
– це було у середній школі, тому не буду знову пояснювати (логарифмічна та експоненціальна функції є оберненими)
та в точці
має скінченну та відмінну від нуля похідну
,
3. Візьмемо точку ![]() . Похідна функції
. Похідна функції ![]() існує (
існує (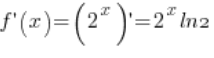 – основні формули для похідних) та у точці
– основні формули для похідних) та у точці ![]() її значення відрізняється від нуля (
її значення відрізняється від нуля (![]() ).
).
тоді в відповідній точці
точка
4. Відповідна точці ![]() точка
точка ![]() є значенням функції
є значенням функції ![]() у точці
у точці ![]() , а саме
, а саме 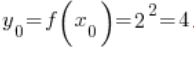 .
.
Отже:
![]()
існує похідна оберненої функції
5. Справді, обернена функція є ![]() , її похідна дорівнює:
, її похідна дорівнює: 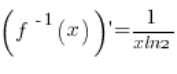 (за основними формулами похідних). У точці
(за основними формулами похідних). У точці ![]() похідна існує і дорівнює:
похідна існує і дорівнює:
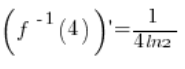
і її значення у точці
дорівнює
.
6. Дійсно, обчислене в пункті 5. 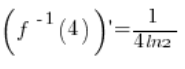 дорівнює:
дорівнює:
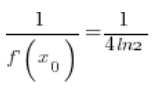 (
(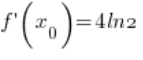 – я обчислив це в пункті 3.)
– я обчислив це в пункті 3.)
Отже, Теорема знову “працює” 🙂
Доведення теореми про похідну оберненої функції
Доведемо цю теорему, посилаючись на геометричне трактування похідної функції в точці. Як пам’ятаємо, значення похідної функції в точці – це тангенс кута нахилу дотичної до графіка функції в цій точці.
На графіку це виглядало б так:
 Значення похідної в точці
Значення похідної в точці ![]() ми визначили на попередніх лекціях як тангенс кута
ми визначили на попередніх лекціях як тангенс кута ![]()
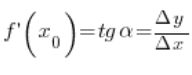
Тепер зауважимо цікаву річ: графік оберненої функції до ![]() можна представити на точно такому ж графіку, тільки треба пам’ятати, що читаємо його “навпаки” – тобто, начебто аргументам y призначаємо значення x (таким чином, приростом аргументів оберненої функції є
можна представити на точно такому ж графіку, тільки треба пам’ятати, що читаємо його “навпаки” – тобто, начебто аргументам y призначаємо значення x (таким чином, приростом аргументів оберненої функції є ![]() , а приростом відповідних їй значень є
, а приростом відповідних їй значень є ![]() ):
):
 Зауважимо, що значення похідної цієї оберненої функції в точці
Зауважимо, що значення похідної цієї оберненої функції в точці ![]() дорівнює:
дорівнює:
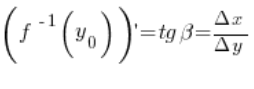
Отже, можна бачити, що значення похідної з функції та значення похідної її оберненої функції це тангенси кутів у тому самому прямокутному трикутнику.
А такі тангенси кутів у прямокутному трикутнику (як ми пам’ятаємо зі школи) пов’язані залежністю:
![]()
Тобто (після поділу з обох сторін на ![]() ):
):
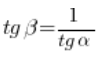
І з цього випливає висновок нашої теореми, а саме:
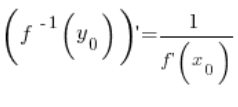
🙂
КІНЕЦЬ ДОВЕДЕННЯ
Виведення формул для похідних за допомогою теореми про похідну оберненої функції
Приклад 3
Виведіть формулу для похідної функції ![]() .
.
Формула, яку ми маємо вивести, це: 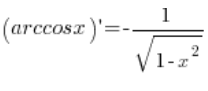 .
.
Наша функція f(x) – це функція arccosx. Обернена до неї функція – це функція ![]() . Похідна з оберненої функції – це
. Похідна з оберненої функції – це 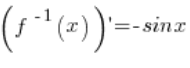 .
.
Згідно з теоремою про похідну оберненої функції, значення похідної з оберненої функції в точці ![]() дорівнює зворотності значення похідної з функції в точці
дорівнює зворотності значення похідної з функції в точці ![]() :
:
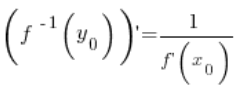
Таким чином, у будь-якій точці ![]() :
:
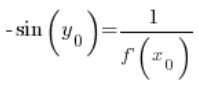
Після перетворення:
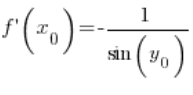
Використовуючи тригонометричну одиницю, можемо вивести, що: 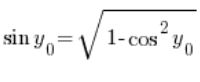 , отже, маємо:
, отже, маємо:
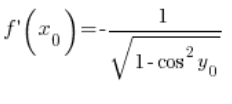
Тепер увага: ![]() це значення функції
це значення функції ![]() у точці
у точці ![]() , тобто
, тобто 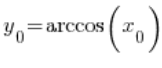 . Отже:
. Отже:
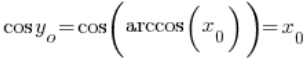 – оскільки косинус і арккосинус – це обернені функції, отже, маємо:
– оскільки косинус і арккосинус – це обернені функції, отже, маємо:
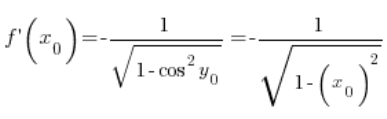 у будь-якій точці
у будь-якій точці ![]() (звичайно, виконуючи умови з областю визначення, яке я знехтував), отже, наша формула
(звичайно, виконуючи умови з областю визначення, яке я знехтував), отже, наша формула 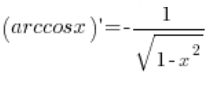 була таким чином доведена.
була таким чином доведена.
Приклад 4
Виведіть формулу для похідної функції ![]() .
.
Формула, яку ми маємо вивести, це: 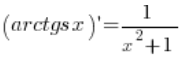 .
.
Наша функція f(x) – це функція arctgx. Обернена до неї функція – це функція ![]() . Похідна з оберненої функції – це
. Похідна з оберненої функції – це 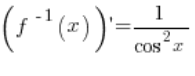 .
.
Згідно з теоремою про похідну оберненої функції, значення похідної з оберненої функції в точці ![]() дорівнює зворотності значення похідної з функції в точці
дорівнює зворотності значення похідної з функції в точці ![]() :
:
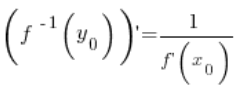
Таким чином, у будь-якій точці ![]() :
:
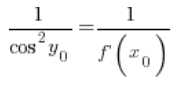
Після перетворення:
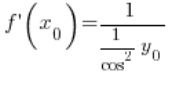
Використовуючи тригонометричну одиницю, можемо перетворити це далі:
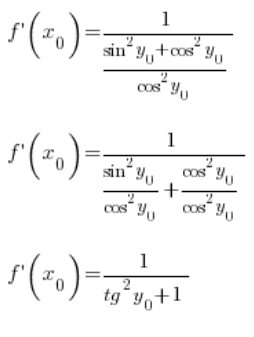
Тепер увага: ![]() це значення функції
це значення функції ![]() в точці
в точці 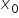 , а саме
, а саме 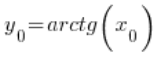 . Отже:
. Отже: 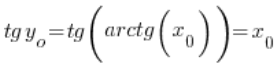 – оскільки тангенс і арктангенс є оберненими функціями, отже, маємо:
– оскільки тангенс і арктангенс є оберненими функціями, отже, маємо:
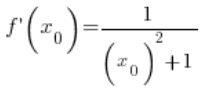 у будь-якій точці
у будь-якій точці ![]() (звичайно, виконуючи умови з областю визначення, яке я знехтував), отже, наша формула
(звичайно, виконуючи умови з областю визначення, яке я знехтував), отже, наша формула 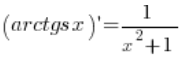 була таким чином доведена.
була таким чином доведена.
КІНЕЦЬ
Пишучи цей пост, я використовував…
1. “Рахунок диференціальний і інтегральний. Том І.” G.M. Фіхтенгольц. Вид. 1966.
Натисніть тут, щоб згадати, як виводити формули для похідних з визначення (попередня Лекція) <–
Натисніть тут, щоб побачити, як можна довести властивості похідних (наступна Лекція) –>
Натисніть тут, щоб повернутися на головну сторінку з лекціями про похідні
