Підстановки Ейлера – кому це потрібно?
Підстановки Ейлера у невизначених інтегралах це те, що вводять після раціональних інтегралів, тригонометричних інтегралів і інтегралів з коренями (або згідно з деякими класифікаціями: “ірраціональних інтегралів”). Це означає, що більшість студентів не матиме задоволення з ними зіткнутися, я також не включив їх до мого Курсу Невизначених Інтегралів.
Але є досить велика група студентів на математичних напрямках, або справді, справді “сильних” з математики, які мають зіткнутися з підстановками Ейлера, і тих (а також зацікавлених) запрошую. Обговорю всі три типи підстановок Ейлера (у цьому пості візьмуся за перший тип) і до кожного зроблю по одному прикладу.
Поїхали.
Які інтеграли розв’язуємо підстановками Ейлера?
Підстановками Ейлера ми розбиваємо інтеграли типу:
…тобто якісь довільні зв’язки 
і 
. Таким чином, їх можна розглядати як певне “продовження” теми інтегралів з коренями (“ірраціональних”).
Підстановками Ейлера ми розбиваємо інтеграли, які не можна вирішити простіше, звісно. Наприклад, інтеграл:
це є інтеграл, у якому маємо зв’язок і , але його можна вирішити дуже просто через дурне підставлення: 
. Тож не стріляємо з гармати по горобцях і в таких простих інтегралах не мучимося з Ейлером.
Візьмімо ж інтеграл:
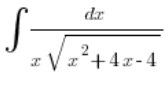
Бачимо, що ситуація серйозніша, справу не вирішать нам знайомі раніше підстановки 
, чи 
(не визначимо з них ).
Потрібна нам нова зброя.
Підстановки Ейлера – I тип
Маючи інтеграл:
в якому 
,
застосовуємо підстановку:
, підносимо обидві сторони до квадрату, члени 
скасовуються (і це мета), визначаємо (в порядку):
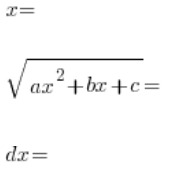
, виражені зв’язками t, підставляємо до вихідного інтегралу:
і маємо інтеграл змінної t (якщо у ньому залишились якісь x-и, то ми допустили помилку) і це раціональний інтеграл.
Увага
Варто ще додати, що на практиці багато студентів знайомі тільки з підстановками Ейлера I типу і тільки до інтегралів типу:
, тобто таких, в яких якби 
Пройдімося по підстановках Ейлера I типу на прикладі:
Приклад 1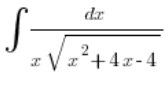
Встановлюємо, що це інтеграл, у якому є зв’язок і . Що його не можна вирішити просто. Що (
це, звісно, коефіцієнт при 
, у нашому прикладі він дорівнює 1).
Отже, ми будемо використовувати підстановку Ейлера I типу.
Здійснюємо підстановку:
тобто просто:
підносимо обидві сторони до квадрату:
Члени з по обидва боки скорочуються (і так має бути кожного разу):
І тепер саме час визначити , і 
(у цьому порядку).
Почнемо з :
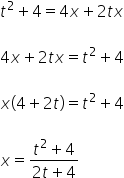
Маємо виражене через змінну t. Тепер черга на , тобто у нашому прикладі: 
.
Повертаємося до нашого першого підстановки, де було:
Тепер ми вже знаємо (бачите, чому важливий порядок, правда?), тому можемо написати:
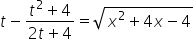
тобто:
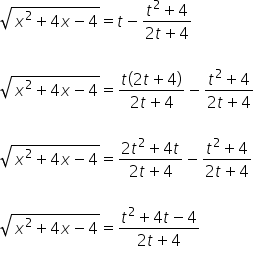
Таким чином, маємо виражене через змінну 
.
В кінці , яке отримуємо просто диференціюючи обидві сторони визначеного :
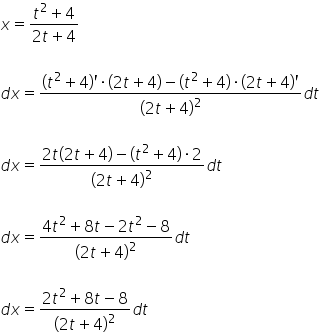
І таким чином ми визначаємо . Отже, маємо:
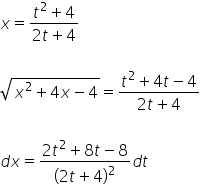
Вставляємо це все до вихідного інтегралу:
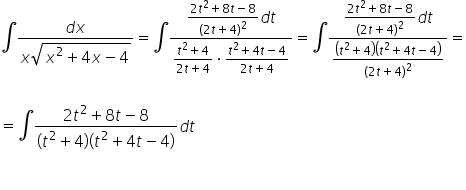
На перший погляд, це здається нудним, клопітким, але вже знаним і схематичним раціональним інтегралом (розклад на прості дроби, другий множник у знаменнику можна розкласти ще більше). Зазвичай так воно і є, але в цьому конкретному прикладі ми матимемо трохи щастя, і пробиватися через 3 сторінки розрахунків A4 нам буде заощаджено:
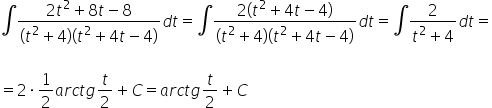
Як повернутися до підстановки? Ми мали на початку:
Звідси, звичайно:
Отже, наш результат:
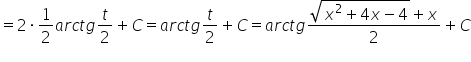
Продовження слідує. (ми ще маємо два типи підстановок Ейлера, що якщо коефіцієнт не більший за нуль?).
