Podstawienia Eulera – komu to potrzebne?
Podstawienia Eulera w całkach nieoznaczonych są następną rzeczą, którą wprowadza się po całkach wymiernych, całkach trygonometrycznych i całkach z pierwiastkami (albo według niektórych klasyfikacji: “całkach niewymiernych”). Co oznacza, że większość studentów nie będzie miała przyjemności się z nimi spotkać, nie ująłem ich także w moim Kursie Całek Nieoznaczonych .
Pozostaje jednak całkiem spora grupa studentów na kierunkach matematycznych, albo naprawdę, naprawdę “mocnych” matematycznie, którzy z podstawieniami Eulera muszą się zmierzyć i tych (a także ciekawych) zapraszam. Omówię wszystkie trzy rodzaje podstawień Eulera (w tym poście wezmę się za I rodzaj) i do każdego zrobię po jednym przykładzie.
Jedziemy.
Jakie całki rozwiązujemy podstawieniami Eulera?
Podstawieniami Eulera rozwalamy całki typu:
…czyli jakieś dowolne związki 
i 
. Można je więc potraktować jako pewne “przedłużenie” tematu całek z pierwiastkami (“niewymiernych”).
Podstawieniami Eulera rozwalamy całki, których nie da się rozwiązać prościej, oczywiście. Na przykład całka:
to jest całka, w której mamy związek i , ale można ją rozwiązać bardzo prosto przez głupie podstawienie: 
. Nie strzelamy więc z armaty do wróbla i w takich prostych całkach nie męczymy się Eulerem.
Weźmy jednak całkę:
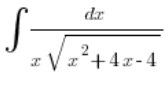
Widzimy, że sytuacja jest poważniejsza, sprawy nie rozwiążą nam znane wcześniej podstawienia 
, czy 
(nie wyznaczymy z nich ).
Potrzebujemy nowej broni.
Podstawienia Eulera – I rodzaj
Mając całkę:
w której 
,
stosujemy podstawienie:
, podnosimy obie strony do kwadratu, składniki 
się skracają (i o to chodzi), wyznaczamy (w kolejności):
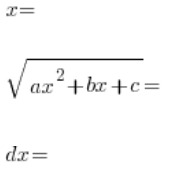
, wyrażone związkami t, podstawiamy do całki wyjściowej:
i mamy całkę zmiennej t (jeśli ostały nam się w niej jakieś x-sy, to popełniliśmy błąd) i jest to całka wymierna.
Uwaga
Warto jeszcze dodać, że w praktyce wielu studentów ma wprowadzone podstawienia Eulera tylko I rodzaju i tylko do całek typu:
, czyli takich, w których jakby 
Prześledźmy podstawienia Eulera I rodzaju w akcji, na przykładzie:
Przykład 1
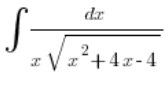
Stwierdzamy, że jest to całka, w której jest związek i . Że nie da się rozwiązać ją prosto. Że (
to oczywiście współczynnik przy 
, w naszym przykładzie jest on równy 1).
Czyli brykać będziemy podstawieniem Eulera I rodzaju.
Podstawiam:
czyli po prostu:
podnoszę obie strony do kwadratu:
Składniki z po obu stronach się skracają (i tak ma właśnie być za każdym razem):
No i teraz właśnie trzeba wyznaczyć , i 
(w tej kolejności).
Zaczniemy od :
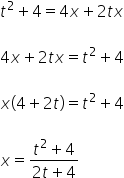
Mamy wyrażone zmienną t. Teraz kolej na , czyli w naszym przykładzie: 
.
Wracamy się do naszego pierwszego podstawienia, w którym było:
Teraz znamy już (widać, dlaczego ważna jest kolejność, prawda?), możemy więc napisać:
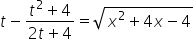
czyli:
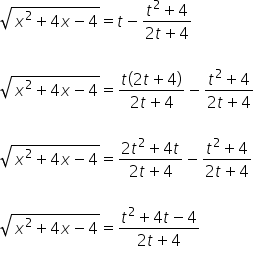
Mamy więc wyrażone zmienną 
.
Na koniec , które bierzemy już po prostu różniczkując obie strony wyznaczonego :
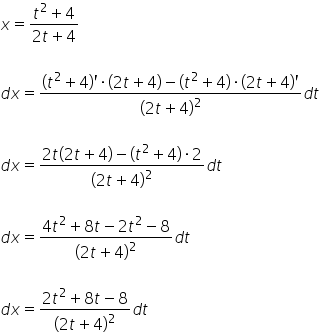
I w ten sposób wyznaczamy . Mamy więc:
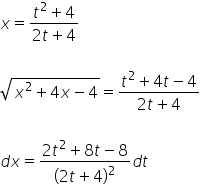
Wstawiamy to wszystko do całki wyjściowej:
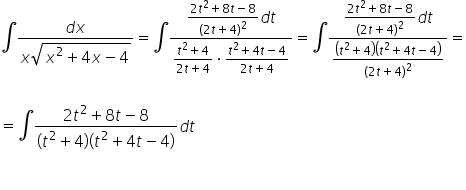
Na pierwszy rzut oka wygląda nam to na nudną, żmudną, ale już znana i schematyczna całka wymierna (rozkład na ułamki proste, drugi czynnik w mianowniku da się jeszcze bardziej rozłożyć). Na ogół tak jest, ale w tym konkretnym przykładzie będziemy mieli trochę szczęścia i przebijanie się przez 3 strony a4 obliczeń zostanie nam oszczędzone:
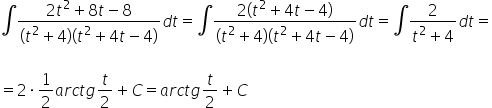
Jak wrócić się podstawieniem? Mieliśmy na początku:
Stąd oczywiście:
Czyli nasz wynik to:
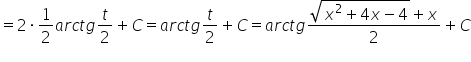
CDN. (mamy jeszcze dwa rodzaje podstawień Eulera, co jeśli współczynnik nie jest większy od zera?).
14 Komentarzy
student
mam nadzieję że zarabia pan na swojej działalności kupę kasy, bo naprawdę pomaga pan masie osób
Integral Love
całki są super
Ale to podstawienie nie jest głupie ;-;
wojtek
Jak policzyć taką całkę:
Integral(1/[x+(x^2+x+1)^1/2])dx
Mariusz
Mógłbyś napisać coś o \interpretacji geometrycznej tych podstawień
chociażby na wypadek gdyby ktoś je zapomniał
Ik
Spotkałam się z takim zapisem podstawienia Eulera I rodzaju: [/latex]sqrt{ax^{2}+bx+c}=\pm [/latex]sqrt{a}+t
Kiedy używamy „+” a kiedy „-„?
Ik
[/latex]sqrt{ax^{2}+bx+c}=\pm[/latex]sqrt{a}x+t
Nie wiem dlaczego nie wyświetla się poprawnie :/
Mariusz
Całki postaci \int{Rleft(x,sqrt{ax^2+bx+c}mbox{d}x}
można przedstawic jako sumę trzech całek \int{R_{1}\left(xright)mbox{d}x}+\int{R_{2}\left(sqrt{ax^2+bx+c}right)mbox{d}\sqrt{ax^2+bx+c}}+\int{R_{3}{\left(frac{x+\frac{b}{2a}}{\sqrt{ax^2+bx+c}}right)}mbox{d}\frac{x+\frac{b}{2a}}{\sqrt{ax^2+bx+c}}}
Podobno można tego dokonac drogą algebraiczną
Mateusz
Witam. Zbiór elementarnych kursów, które są realizowane na każdej uczelni, już zagościł w tym serwisie:) Zostało prawdopodobieństwo, statystyka ale z tym jest różnie na uczelniach. Ja miałem jeszcze na koniec ostatniego semestru (kier. energetyka) takie zagadnienia jak: funkcje zespole, całki funkcji zespolonych, badanie holomorficzności funkcji. Kursy można oczywiście rozszerzać. Wszystko zależy od chęci Pana Krystiana. Może w przyszłości jakiś podstawowy kurs z 3DGrapher’a albo MATLABA? Pozdrawiam
Dominik
Ja proponuje prawdopodobieństwo jest na każdym profilu studiów matematycznych a statystyka nie
Mateusz
krystian, dawaj na pg flache obalic!
Ania
Super są te Pana kursy:) Można zapytać czy ma Pan w planie jeszcze jakieś kursy? A jeśli tak, to jaki temat będzie obejmował następny :)?
Pozdrawiam,
Ania
Krystian Karczyński
Dzięki 🙂 Tak, będę tworzył następ\ne Kursy. Co do następ\nego myślałem o Statystyce, ale można najpierw zrobię Prawdopodobieństwo, nie zdecydowałem się jeszcze…
Janusz
Fajne, więcej takich. Dzięki.