Dlaczego wykres funkcji nie może mieć dwóch asymptot ukośnych przy x dążącym do plus nieskończoności?

Krystian Karczyński

Założyciel i szef serwisu eTrapez.

Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.

Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.

Do odpowiedzi na postawione w tytule pytanie nie potrzebujemy sięgać aż do definicji asymptoty ukośnej, wystarczy nam sama wiedza o tym, czym jest funkcja.

Jak często w matematyce bywa – wyobrazimy sobie roboczo, że wykres funkcji MA dwie różne asymptoty ukośne przy i pokażemy, że przyjmując takie założenie dojdziemy na pewno do sprzeczności, zatem tego założenia przyjąć nie można.

Wykres

Na wykresie te asymptoty mogły by wyglądać na przykład tak:

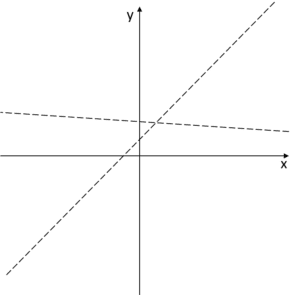A wykres funkcji powinien zbliżać się do tych asymptot przy , zatem wyglądać będzie następująco:

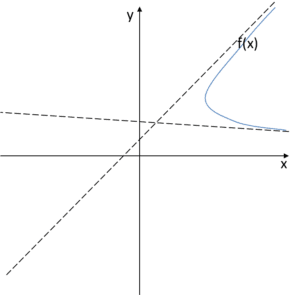I co? Może tak być? Czy tak wyglądać może wykres funkcji? Czy jednak mamy tu jakiś problem?

Problem

Oczywiście mamy. To, co jest powyżej nie może być wykresem funkcji. Sięgnijmy do źródeł, funkcja z definicji to przyporządkowanie, które każdemu argumentowi x przyporządkowuje dokładnie jedną wartość y. A co wynika z naszego wykresu?

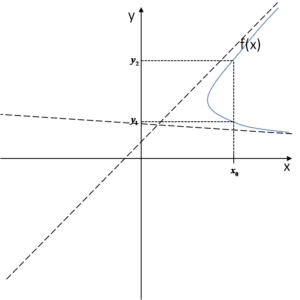Odczytać można z niego, że na przykład argumentowi przyporządkowane są dwie wartości – i . A tak nie może być w wykresie funkcji, bo w niej każdemu argumentowi x odpowiadać musi tylko jedna wartość y.

Zatem funkcja nie może mieć dwóch różnych asymptot ukośnych przy . Całe rozumowanie można powtórzyć odpowiednio dla  🙂