Why can’t a function graph have two oblique asymptotes as x approaches positive infinity?
Krystian Karczyński
Founder and General Manager of eTrapez.
Graduate of Mathematics at Poznan University of Technology. Mathematics tutor with many years of experience. Creator of the first eTrapez Courses, which have gained immense popularity among students nationwide.
He lives in Szczecin, Poland. He enjoys walks in the woods, beaches and kayaking.
To answer the question posed in the title, we don’t need to go back to the definition of an oblique asymptote, we just need to know what a function is.
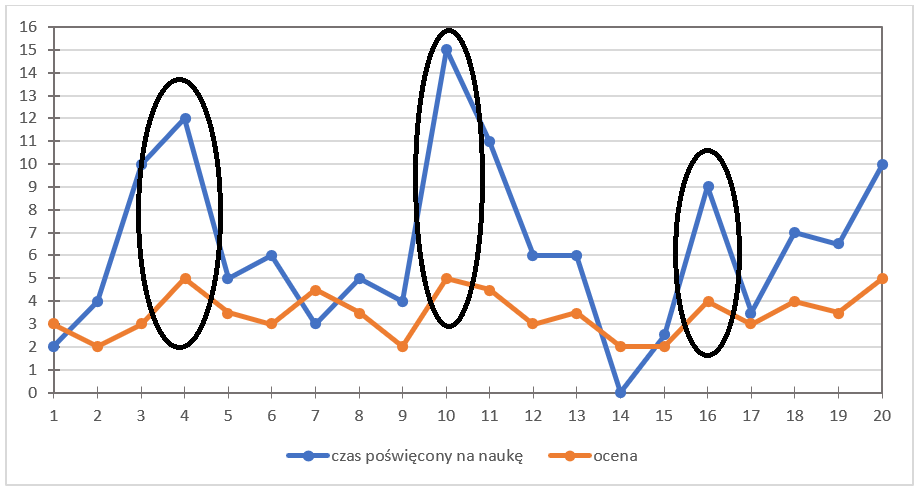
As is often the case in mathematics, let’s imagine that the graph of the function HAS two different oblique asymptotes at 
, and show that assuming this will definitely lead us to a contradiction, so this assumption cannot be accepted.
Graph
In the graph, these asymptotes might look like this:
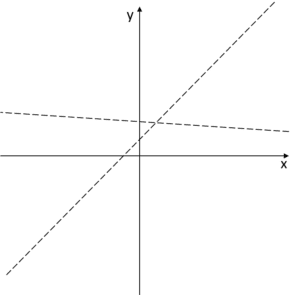And the graph of the function should approach these asymptotes at , so it will look like this:
And what? Can it be like this? Can the graph of a function look like this? Or do we have a problem here?
Problem
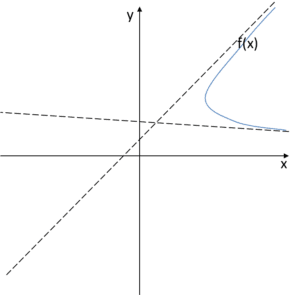
Of course, we have a problem. What is shown above cannot be the graph of a function. Let’s go back to the basics, a function by definition is a mapping that assigns exactly one y value to each x argument. And what does our graph show?
We can see that, for example, the argument 
is assigned two values – 
and 
. And that can’t happen in a function graph, because each x argument must correspond to only one y value.
Therefore, a function cannot have two different oblique asymptotes at . The entire reasoning can be repeated accordingly for 
🙂
Are you looking for college or high school math tutoring? Or maybe you need a course that will prepare you for the final exam?
We are "eTrapez" team. We teach mathematics in a clear, simple and very precise way - we will reach even the most knowledge-resistant students.
We have created video courses translated in an easy, understandable language, which can be downloaded to your computer, tablet or phone. You turn on the video, watch and listen, just like during private lessons. At any time of the day or night.
