
Układ równań z parametrem do wyznaczenia
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
![]() Oblicz parametr 'a’ w powyższym układzie równań wiedząc, że jest on sprzeczny.
Oblicz parametr 'a’ w powyższym układzie równań wiedząc, że jest on sprzeczny.
Zamiast schematycznie rozpoczynać liczeniem rzędu macierzy głównej, wyznaczmy rząd macierzy uzupełnionej:
![]() …jest on równy dwa, bo w tej macierzy można wyodrębnić niezerowy wyznacznik drugiego stopnia (a większego już nie da rady):
…jest on równy dwa, bo w tej macierzy można wyodrębnić niezerowy wyznacznik drugiego stopnia (a większego już nie da rady):
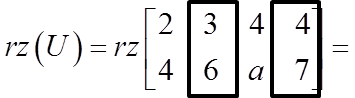
![]() Rząd macierzy uzupełnionej jest więc równy 2.
Rząd macierzy uzupełnionej jest więc równy 2.
Zastosowanie twierdzenia Kroneckera-Capellego
Jaki powinien więc wyjść rząd macierzy głównej?
Wiemy, że układ jest sprzeczny, a z twierdzenia Kroneckera-Capellego wiemy, że będzie on sprzeczny, kiedy rząd macierzy głównej będzie różny od rzędu macierzy uzupełnionej. Wiemy też, że rząd macierzy głównej jest zawsze mniejszy lub równy od rzędu macierzy uzupełnionej (macierz główna zawiera się w uzupełnionej). Czyli rząd macierzy głównej powinien wyjść 1 albo 0 (żeby był różny od rzędu macierzy uzupełnionej).
Rząd macierzy głównej równy będzie:
![]() Widzimy, że nie będzie on na pewno równy 0 (tylko i wyłącznie rząd macierzy zerowej równy jest 0) – powinien więc on być równy 1. Rząd będzie równy jeden, kiedy wiersz pierwszy i drugi będą proporcjonalny (wtedy jeden z nich wykreślimy). Widać, że wiersz pierwszy przemnożony przez dwa daje wiersz drugi, jeśli tylko a równe będzie 8.
Widzimy, że nie będzie on na pewno równy 0 (tylko i wyłącznie rząd macierzy zerowej równy jest 0) – powinien więc on być równy 1. Rząd będzie równy jeden, kiedy wiersz pierwszy i drugi będą proporcjonalny (wtedy jeden z nich wykreślimy). Widać, że wiersz pierwszy przemnożony przez dwa daje wiersz drugi, jeśli tylko a równe będzie 8.
Zatem szybko i bez wielkich obliczeń dochodzimy do odpowiedzi:
![]()
Bestsellery

Kurs Statystyka
Studia / Autor: mgr Krystian Karczyński
Pierwotna cena wynosiła: 49,00 zł.34,30 złAktualna cena wynosi: 34,30 zł.

Kurs Macierze
Studia / Autor: mgr Krystian Karczyński
Pierwotna cena wynosiła: 49,00 zł.34,30 złAktualna cena wynosi: 34,30 zł.

Kurs Równania Różniczkowe
Studia / Autor: mgr Krystian Karczyński
Pierwotna cena wynosiła: 49,00 zł.34,30 złAktualna cena wynosi: 34,30 zł.

Kurs Wytrzymałość Materiałów
Studia / Autor: mgr inż. Adam Kasprzak
Pierwotna cena wynosiła: 49,00 zł.34,30 złAktualna cena wynosi: 34,30 zł.
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.






a co w przypadku, gdy mamy rozwiązać układ w zależności od parametru, a ich jest dużo więcej:
x + (p-2)y – 2pz = 4
px + (3-p)y + 4z = 1
(1+p)x + y + 2(2-p)z = 7
???
Witam, tutaj napisałem co nie coś ma ten temat:
https://blog.etrapez.pl/macierze/rzad-macierzy-w-ukladach-rownan-liniowych-z-parametrem/
Ta strona nie istnieje :<
Poprawiłem link, przepraszam.