Currently Empty: zł0.00
Krystian Karczyński- 17 września 2010
- Comment 4
Oblicz parametr 'a’ w powyższym układzie równań wiedząc, że jest on sprzeczny.
Zamiast schematycznie rozpoczynać liczeniem rzędu macierzy głównej, wyznaczmy rząd macierzy uzupełnionej:
…jest on równy dwa, bo w tej macierzy można wyodrębnić niezerowy wyznacznik drugiego stopnia (a większego już nie da rady):
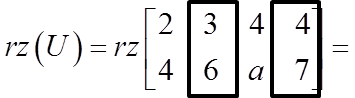
Rząd macierzy uzupełnionej jest więc równy 2.
Zastosowanie twierdzenia Kroneckera-Capellego
Jaki powinien więc wyjść rząd macierzy głównej?
Wiemy, że układ jest sprzeczny, a z twierdzenia Kroneckera-Capellego wiemy, że będzie on sprzeczny, kiedy rząd macierzy głównej będzie różny od rzędu macierzy uzupełnionej. Wiemy też, że rząd macierzy głównej jest zawsze mniejszy lub równy od rzędu macierzy uzupełnionej (macierz główna zawiera się w uzupełnionej). Czyli rząd macierzy głównej powinien wyjść 1 albo 0 (żeby był różny od rzędu macierzy uzupełnionej).
Rząd macierzy głównej równy będzie:
Widzimy, że nie będzie on na pewno równy 0 (tylko i wyłącznie rząd macierzy zerowej równy jest 0) – powinien więc on być równy 1. Rząd będzie równy jeden, kiedy wiersz pierwszy i drugi będą proporcjonalny (wtedy jeden z nich wykreślimy). Widać, że wiersz pierwszy przemnożony przez dwa daje wiersz drugi, jeśli tylko a równe będzie 8.
Zatem szybko i bez wielkich obliczeń dochodzimy do odpowiedzi:
Renata
a co w przypadku, gdy mamy rozwiązać układ w zależności od parametru, a ich jest dużo więcej:
x + (p-2)y – 2pz = 4
px + (3-p)y + 4z = 1
(1+p)x + y + 2(2-p)z = 7
???
Krystian Karczyński
Witam, tutaj napisałem co nie coś ma ten temat:
https://blog.etrapez.pl/macierze/rzad-macierzy-w-ukladach-rownan-liniowych-z-parametrem/
Konrad
Ta strona nie istnieje :<
Krystian Karczyński
Poprawiłem link, przepraszam.