En los problemas más difíciles sobre integrales definidas, siempre es bueno mantenerse alerta – una tarea que parece muy difícil puede resolverse con una fórmula simple de la escuela secundaria.
Problema sobre el volumen de un sólido de revolución
Digamos que necesitamos calcular el volumen de un sólido formado por la rotación de una curva:
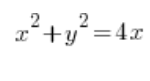
girando (vale, digamos «rotando») alrededor del eje OX. Unos cuantos movimientos ordenados conocidos desde la secundaria…
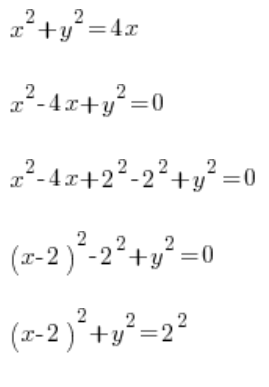
…y nos damos cuenta de que nuestra curva es simplemente un círculo pequeño con el centro en el punto (2,0) y radio de 2. ¿Y ahora qué? Derivamos y de la fórmula y empujamos la integral definida: 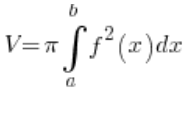 ?
?
Solución
No… Detengámonos un momento. Respiremos hondo. Pensemos. Un pequeñito círculo… Se rota… ¿Qué resultará de tal rotación? Obviamente, una esfera. Conocemos la fórmula para el volumen de una esfera desde la secundaria:
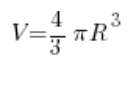
Ya conocemos el radio (es dos), lo que significa:
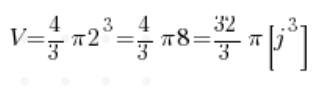
Y ahí tenemos la respuesta, sin siquiera tocar las integrales 🙂


