Deriving Formulas for Derivatives
Derivative formulas didn’t just come from outer space, they are actually derived from the definition of a derivative:
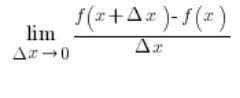
The Derivative of the Square Root of x
Let’s derive the formula for the derivative of the square root of x: 
. We should get: 
(so say the basic derivative formulas – formula number 5).
We have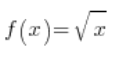 
. Let’s get to it. After substituting into the derivative formula from the definition, we will receive:
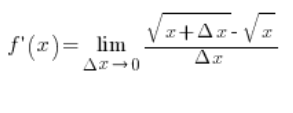
By multiplying the numerator and the denominator in the following way…
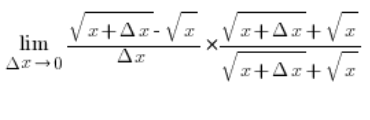
…and using the formula for perfect square trinomial in the numerator, we will eliminate the irrationality and end up with:
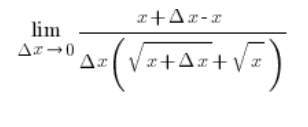
The x’s on top in the numerator will cancel out and we get…
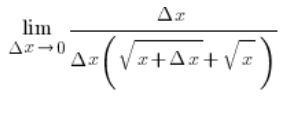
…and after cancelling out 
in the numerator and denominator:
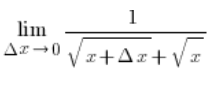
Since 
it means that:
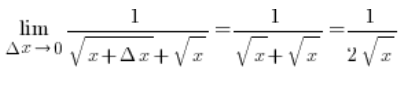
So, we are home. The formula for the derivative has been derived.
More Examples
Feel free to play around with other formulas, I encourage you!
Derivatives and Function Analysis Course
You can also find various step-by-step calculated cases in my Derivatives and Function Analysis Course.
More General Cases
The task of deriving a formula for a derivative always comes down to calculating the appropriate limit, where ‘x’ is treated as a constant. It might be easier or harder, but you can use methods and tricks you’re already familiar with from calculating function limits.
With one caveat.
Unfortunately – the l’Hôpital’s Rule is off the table. Why? Precisely because it utilizes derivatives.
Let me remind you of your task – you need to compute the derivative of a function from the definition, without knowing the formula. And l’Hôpital’s Rule often uses derivative formulas!
