Homogene lineare Gleichungssysteme sind solche Systeme, bei denen alle freien Glieder gleich 0 sind. Sie sehen so aus:
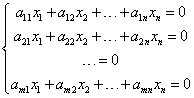
Zum Beispiel:
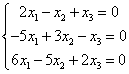
Mögliche Anzahl von Lösungen in linearen Gleichungssystemen
Erinnern wir uns, dass in jedem linearen Gleichungssystem drei Situationen möglich sind:
- Das System hat eine Lösung (wenn der Rang der Matrix der Hauptmatrix = der Rang der Matrix der erweiterten Matrix = Anzahl der Unbekannten im System:
) - Das System hat unendlich viele Lösungen (wenn der Rang der Matrix der Hauptmatrix = der Rang der Matrix der erweiterten Matrix und kleiner ist als die Anzahl der Unbekannten im System: )
- Das System hat keine Lösung (wenn der Rang der Matrix der Hauptmatrix nicht gleich dem Rang der erweiterten Matrix ist)
Die erweiterte Matrix ist die Hauptmatrix mit einer hinzugefügten Spalte der freien Glieder. Im Fall eines homogenen Systems wird dies eine Spalte mit lauter Nullen sein. Beim Berechnen der Ränge kann sie einfach gestrichen werden, wodurch nur die Hauptmatrix übrig bleibt.
In unserem Beispiel ist der Rang der Hauptmatrix gleich:
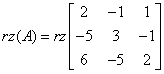
Und der Rang der erweiterten Matrix:
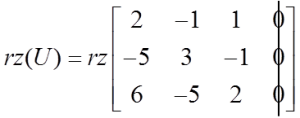
In dem Beispiel sehen wir, dass 
und es ist zu erkennen, dass dies immer so sein wird, in jedem homogenen System.
Mögliche Anzahl von Lösungen in homogenen linearen Gleichungssystemen
Folglich gibt es in homogenen Gleichungssystemen nur die Fälle 1 oder 2. Das System wird immer Lösungen haben, die Frage ist nur, ob es eine Lösung oder unendlich viele Lösungen gibt.
Gehen wir weiter.
Definieren wir etwas, das als „Nullösung“ bezeichnet wird. Eine Nullösung ist eine Lösung, bei der alle Unbekannten gleich 0 sind.
Bei Betrachtung homogener Gleichungssysteme kann man feststellen:
Die Nullösung ist immer eine Lösung des homogenen Systems.
Das ist leicht zu überprüfen: Setzt man alle Unbekannten in den Gleichungen auf null, sieht man klar, dass jede Gleichung des homogenen Systems erfüllt ist, immer und in jedem homogenen System.
Wenn wir also wissen, dass ein homogenes lineares Gleichungssystem eine Lösung hat (das ist der Fall, wenn 
), dann wissen wir auch, dass dies sicherlich die Nullösung ist.
Wenn wir hingegen wissen, dass ein homogenes lineares Gleichungssystem unendlich viele Lösungen hat (das ist der Fall, wenn 
), dann wissen wir, dass das System die Nullösung hat, aber zusätzlich dazu auch einige Nicht-Nullösungen.
Wenn wir also in einer Aufgabe den Auftrag haben: „Überprüfe, ob das homogene System Nicht-Nullösungen hat“, reicht es aus, zu zeigen, dass es sich um ein unbestimmtes System handelt, bei dem der Rang der Hauptmatrix und der erweiterten Matrix kleiner ist als die Anzahl der Unbekannten.
In einigen Systemen ist das sehr einfach, zum Beispiel hier:
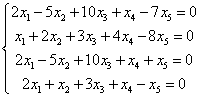
Die Hauptmatrix des Systems hätte 4 Zeilen und 5 Spalten, also wird ihr Rang höchstens 4 sein. Der Rang der erweiterten Matrix ist ebenfalls 4 – wir wissen schon warum. Die Anzahl der Unbekannten ist 5. Daher kann man sofort feststellen, dass das System unbestimmt ist und dass es einige Nicht-Nullösungen für dieses System gibt.
