Sistemas de ecuaciones homogéneas (número de soluciones utilizando el rango de la matriz)
Krystian Karczyński
Fundador y jefe del servicio eTrapez.
Maestro en Matemáticas por la Universidad Tecnológica de Poznań (Polonia). Tutor de matemáticas con muchos años de experiencia. Creador de los primeros Cursos eTrapez, que se han vuelto enormemente populares entre estudiantes de toda Polonia.
Vive en Szczecin (Polonia). Le gusta caminar por el bosque, ir a la playa y hacer kayak.
Los sistemas de ecuaciones lineales homogéneas son aquellos sistemas en los que todos los términos independientes son iguales a 0. Se ven así:
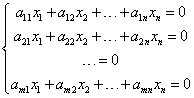
Por ejemplo:
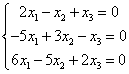
Número posible de soluciones en sistemas de ecuaciones lineales
Recordemos que en cada sistema de ecuaciones lineales hay tres situaciones posibles:
- El sistema tiene una solución (cuando el rango de la matriz principal = rango de la matriz ampliada = número de incógnitas en el sistema:
) - El sistema tiene infinitas soluciones (cuando el rango de la matriz principal = rango de la matriz ampliada y es menor que el número de incógnitas en el sistema: )
- El sistema no tiene soluciones (cuando el rango de la matriz principal no es igual al rango de la matriz ampliada)
La matriz ampliada es la matriz principal con una columna añadida de términos independientes. En el caso de un sistema homogéneo, será una columna de ceros. Al calcular los rangos, se puede simplemente eliminar y obtener así solo la matriz principal.
En nuestro ejemplo, el rango de la matriz principal es:
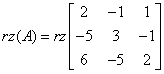
Y el rango de la matriz ampliada:
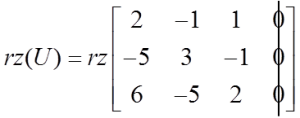
En el ejemplo podemos ver que 
y se puede ver que siempre será así, en cada sistema homogéneo.
Número posible de soluciones en sistemas de ecuaciones lineales homogéneas
Por lo tanto, en los sistemas de ecuaciones homogéneas solo se darán las situaciones 1 o 2. El sistema siempre tendrá soluciones, la única pregunta es si será una solución o infinitas soluciones.
Vamos más allá.
Definamos algo llamado “solución cero”. Llamaremos solución cero a aquella solución en la que los valores de todas las incógnitas son 0.
Al hablar de sistemas de ecuaciones homogéneas, se puede notar que:
La solución cero siempre es una solución del sistema homogéneo.
Esto es fácil de comprobar: si ponemos ceros en todas las incógnitas en las ecuaciones, se puede ver claramente que cada ecuación del sistema homogéneo se cumple, siempre y en cada sistema homogéneo.
Si sabemos que un sistema de ecuaciones lineales homogéneas tiene una solución (y es así cuando 
), también sabemos que esta es seguramente la solución cero.
Si sabemos que un sistema de ecuaciones lineales homogéneas tiene infinitas soluciones (y es así cuando 
), sabemos que el sistema tiene la solución cero, pero además algunas soluciones no nulas.
Si en el ejercicio se nos pide: “comprueba si el sistema homogéneo tiene soluciones no nulas”, basta con demostrar que es un sistema indeterminado, en el que el rango de la matriz principal y el rango de la matriz ampliada es menor que el número de incógnitas.
En algunos sistemas esto es muy sencillo, por ejemplo aquí:
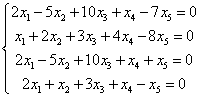
La matriz principal del sistema tendría 4 filas y 5 columnas, por lo que su rango será como máximo 4. El rango de la matriz ampliada es igual – ya sabemos por qué. El número de incógnitas es 5. Por lo tanto, se puede decir inmediatamente que el sistema es indeterminado y que existen algunas soluciones no nulas para este sistema.
¿Buscas clases particulares de matemáticas para nivel universitario o de secundaria? ¿O quizás necesitas un curso que te prepare para el examen de selectividad?
Somos el equipo de eTrapez. Enseñamos matemáticas de manera clara, sencilla y muy detallada - llegamos incluso al más resistente al aprendizaje.
Hemos creado cursos en video explicados en un lenguaje comprensible para descargar en tu computadora, tableta o teléfono. Enciendes la grabación, miras y escuchas, como en las clases particulares. A cualquier hora del día o de la noche.
