Homogeneous systems of linear equations are systems in which all constant terms are equal to 0. They look like this:
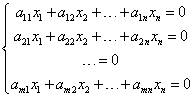
For example:
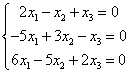
Possible numbers of solutions in systems of linear equations
Let us recall that in any system of linear equations there are three possible situations:
1. The system has 1 unique solution (when the rank of the main matrix = the row of the supplemented matrix = the number of unknowns in the system:
)
2. The system has infinitely many solutions (when the rank of the coefficient matrix = the rank of the augmented matrix and is smaller than the number of variables in the system
)
3. The system has no solutions at all (when the rank of the coefficient matrix is not equal to the rank of the augmented matrix). The augmented matrix is the main matrix with an added column of constant terms. In the case of a homogeneous system, it will be a column with only zeros. In the process of computing the matrix rank, you can simply skip it and get just the coefficient matrix.
In our example above, the rank of the coefficient matrix is equal to:
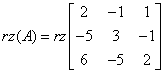And the rank of the augmented matrix:
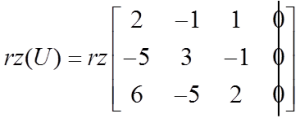
The example shows that
and it is obvious that this will always be the case in every homogeneous system.
Possible numbers of solutions in a homogeneous system
If so, only situations 1 or 2 will occur in the system of homogeneous equations. The system will always have solutions, the only question is whether it will be 1 solution or infinitely many solutions.
Let’s move on.
Let’s define something like a “zero solution”. A zero solution is a solution in which the values of all unknowns are equal to 0.
Speaking about systems of homogeneous equations, it can be noted that:
The zero solution is always the solution of a homogeneous system.
It is easy to check: if we put zeros for all unknowns in the equations, it is clear that every equation of a homogeneous system will be satisfied, always and in every homogeneous system.
So if we know that a homogeneous system of linear equations has one unique solution (and this is the case when ), we also know that this is a zero solution for sure.
If we know that a homogeneous system of linear equations has infinitely many solutions (and this is the case when ), we know that the system has a zero solution, but also some non-zero solutions.
Therefore, if in the task we are asked: “check whether the homogeneous system has non-zero solutions”, it is enough to prove that it is an undefined system in which the order of the coefficient and augmented matrices is smaller than the number of unknowns.
In some systems this is very simple, for example here:
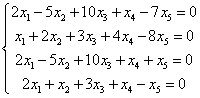The coefficient matrix of the system would have 4 rows and 5 columns, so its rank will be at most 4. The row of the matrix augmented in the same way – we now know why. The number of unknowns (‘n’) is equal 5. We can immediately say that the system is undetermined and that there are some non-zero solutions of this system.
