Grenzwerte von Folgen mit Logarithmen
Krystian Karczyński
Gründer und Chef des Dienstes eTrapez.
Master of Mathematics der Technischen Universität Pozen (Polen). Mathematik-Nachhilfelehrer mit langjähriger Erfahrung. Schöpfer der ersten eTrapez-Kurse, die bei Studenten in ganz Polen große Beliebtheit erlangten.
Lebt in Stettin (Polen). Mag Waldspaziergänge, Strandtage und Kajakfahren.
Für die Grenzwerte vieler Folgen mit Logarithmen kann man sicher die Transformationen und Formeln für Logarithmen aus der Schule anwenden. Zum Beispiel:
Beispiel für den Grenzwert einer Folge mit Logarithmen
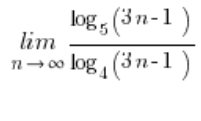
In Situationen, in denen Logarithmen unterschiedliche Basen hatten und man nicht viel damit anfangen konnte, wurden sie auf eine gemeinsame Basis gebracht, indem man die Formel verwendete: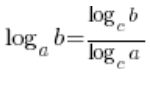 
. Für unseren Grenzwert wird es schön und praktisch sein, diese Basis zu wählen: 
. Dann haben wir den Grenzwert der Folge:
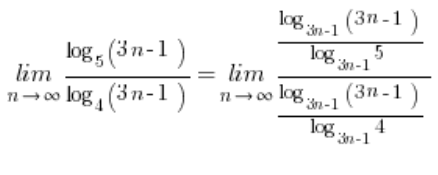
Wir wissen, dass 
, was in unserem Ausdruck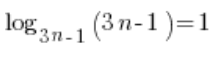 
ist. Daher:
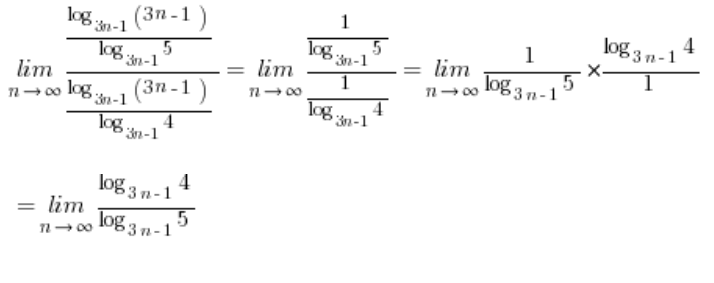
Und dieser Ausdruck, wieder unter Verwendung der Schulformel (diesmal jedoch umgekehrt), wird gleich sein: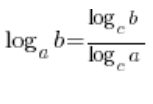 
…
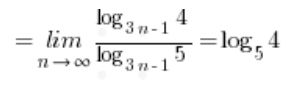
Was natürlich das Ergebnis ist (eine irrationale Zahl).
Es war nicht nötig, irgendwelche Grenzwertmethoden anzuwenden – die Schultransformationen der Logarithmen waren ausreichend.
Willst du mehr über die Berechnung von Grenzwerten wissen? Ich empfehle meinen Kurs 🙂
Suchen Sie nach Mathe-Nachhilfe für das Universitätsniveau oder die Oberstufe? Oder benötigen Sie vielleicht einen Kurs, der Sie auf das Abitur vorbereitet?
Wir sind das Team von eTrapez. Wir unterrichten Mathematik auf eine klare, einfache und sehr detaillierte Weise - wir erreichen sogar diejenigen, die sich am meisten gegen das Lernen sträuben.
Wir haben Kurse in Videoform erstellt, die in einer verständlichen Sprache erklärt sind, zum Herunterladen auf Computer, Tablet oder Handy. Sie starten die Aufnahme, schauen und hören zu, als wären Sie bei der Nachhilfe. Zu jeder Tages- und Nachtzeit.
