Berechne den Parameter ‚a‘ im obigen Gleichungssystem, da er widersprüchlich ist.
Anstatt systematisch mit der Berechnung des Rangs der Hauptmatrix zu beginnen, bestimmen wir den Rang der erweiterten Matrix:
…er ist gleich zwei, denn in dieser Matrix kann man einen nicht-null Determinanten zweiter Ordnung extrahieren (einen größeren bekommt man nicht):
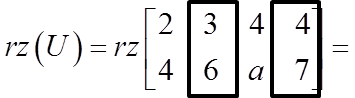
Der Rang der erweiterten Matrix ist also gleich 2.
Anwendung des Kronecker-Capelli-Theorems
Was sollte also der Rang der Hauptmatrix sein?
Wir wissen, dass das System widersprüchlich ist, und aus dem Kronecker-Capelli-Theorem wissen wir, dass es widersprüchlich ist, wenn der Rang der Hauptmatrix von dem der erweiterten Matrix abweicht. Wir wissen auch, dass der Rang der Hauptmatrix immer kleiner oder gleich dem Rang der erweiterten Matrix ist (die Hauptmatrix ist in der erweiterten Matrix enthalten). Also sollte der Rang der Hauptmatrix 1 oder 0 sein (um sich vom Rang der erweiterten Matrix zu unterscheiden).
Der Rang der Hauptmatrix wird sein:
Wir sehen, dass er definitiv nicht 0 ist (nur die Nullmatrix hat einen Rang von 0) – also sollte er 1 sein. Der Rang wird eins sein, wenn die erste und zweite Zeile proportional sind (dann streichen wir eine davon). Wir sehen, dass die erste Zeile mit zwei multipliziert die zweite Zeile ergibt, wenn nur a gleich 8 ist.
Also kommen wir schnell und ohne große Berechnungen zur Antwort:
