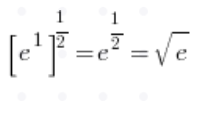Typische Folgen-Grenzen mit einer Formel für die Zahl e
Traditionelle Aufgaben zu Folgen-Grenzen mit einer Formel für die Zahl e führen recht „natürlich“ zu der Formel (ich zeige, wie das geht, in meinem Kurs):
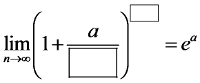Aber was ist, wenn wir statt eines so eleganten Bruchs etwas wie das im Klammerausdruck haben:
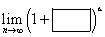Wenn das Rechteck im Klammerausdruck gegen Null geht und das Dreieck im Exponenten gegen Unendlichkeit, haben wir eigentlich ein unbestimmtes Symbol 
– genau der Typ, bei dem wir die Formel mit der Zahl ‚e‘ im Ergebnis verwenden. Was tun?
Nun, erinnern wir uns, dass jeder Ausdruck als Division von Eins durch den Kehrwert dieses Ausdrucks dargestellt werden kann 🙂
Zum Beispiel kann die einfache, höfliche Zahl 2 als geschrieben werden:
Also kann jeder Ausdruck „mit Gewalt“ zu einem Bruch gemacht werden, wenn es wirklich notwendig ist.
Beispiel einer unkonventionellen Grenze mit einer Formel für die Zahl e
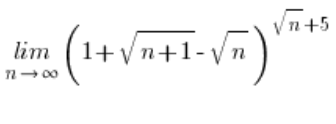
Zuerst sollte gezeigt werden, dass der Ausdruck 
gegen Null geht. Du machst das, indem du die Grenze berechnest:
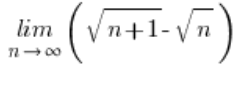– das Ergebnis wird tatsächlich Null sein (du kannst die Methode der Multiplikation mit dem Konjugierten anwenden).
Jetzt ersetzt du:
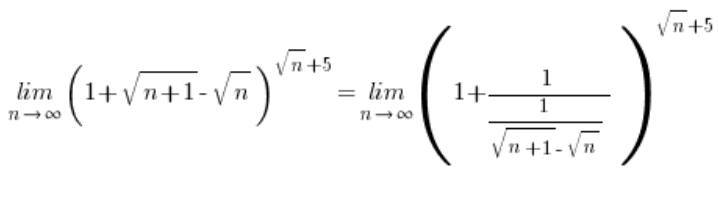
… und machst weiter nach dem bekannten Schema:
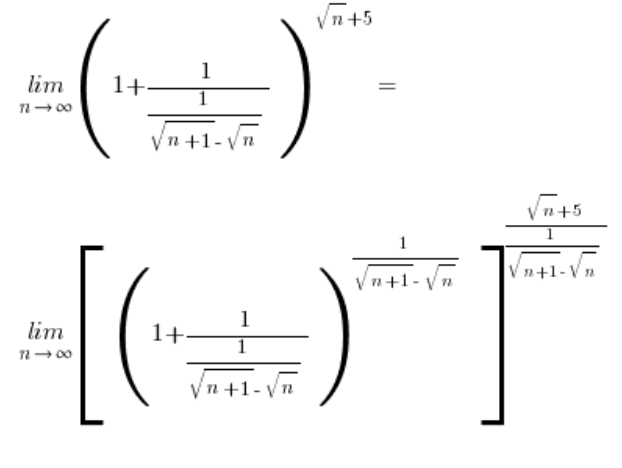
Die Grenze in der großen eckigen Klammer ist: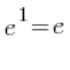 
– gemäß der grundlegenden Formel, bleibt nur noch der letzte Schritt mit:
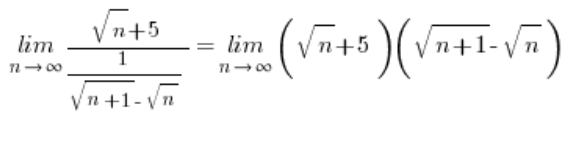
… der nach Anwendung der Multiplikation mit dem Konjugierten mit dem Ergebnis 
endet.
Somit ist die gesamte Grenze gleich:
