Nietypowa granica ciągu ze wzorem na liczbę e w wyniku
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Typowe granice ciągów z wzorem na liczbę e
Tradycyjne zadania na granice ciągu ze wzorem na liczbę e dosyć “naturalnie” doprowadzić do wzoru (pokazuję jak to robić w moim Kursie):
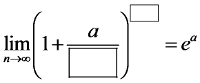Co jednak w sytuacji, kiedy w nawiasie nie mamy takiego zgrabnego ułamka, ale coś typu:
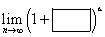Jeśli prostokącik w nawiasie zbiega do zera, a trójkącik w wykładniku rozbiega do nieskończoności mamy tu właściwie symbol nieoznaczony 
– czyli dokładnie taki, w którym stosujemy wzór z liczbą ‘e’ w wyniku. Co robić?
No cóż pamiętajmy, że dowolne wyrażenie da się przedstawić jako dzielenie jedynki przez odwrotność tego wyrażenia 🙂
Na przykład zwykłą, grzeczną liczbę 2 można zapisać jako:
Tak więc z każdego wyrażenia da się “na siłę” zrobić ułamek, jeśli naprawdę trzeba.
Przykład nietypowej granicy z wzorem na liczbę e
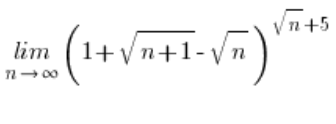
Najpierw wypadało by wykazać, że wyrażenie 
dąży do zera. Zrobisz to, licząc granicę:
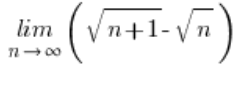– wyjdzie faktycznie równa zero (można zastosować metodę mnożenia przez sprzężenie).
Teraz zamieniasz:
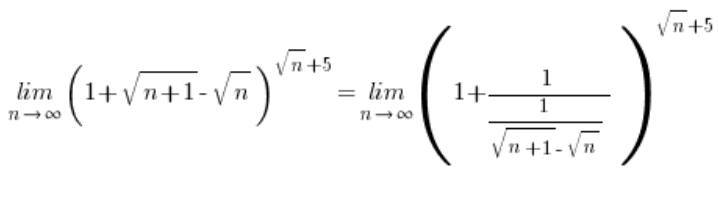
… i dalej już według znanego schematu:
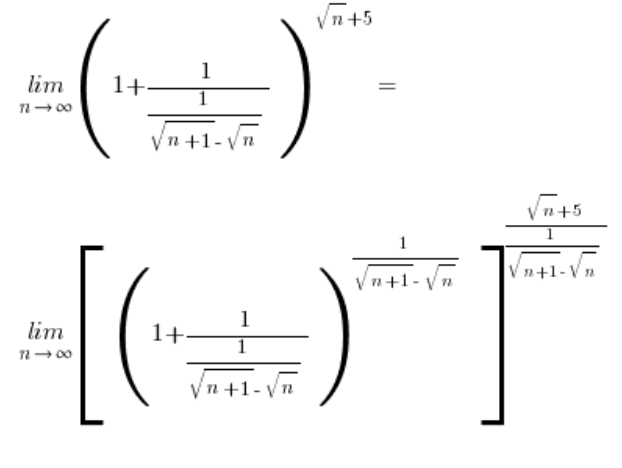
Granica w wielgachnym nawiasie kwadratowym wynosi: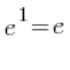 
– zgodnie z podstawowym wzorem, pozostaje już tylko przeprawa z:
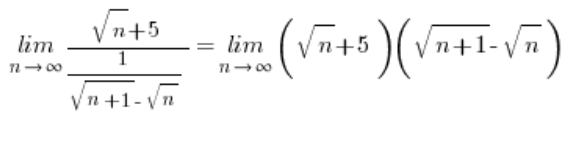
… która po zastosowaniu mnożenia przez sprzężenie zakończy się wynikiem 
.
Cała granica więc równa będzie:
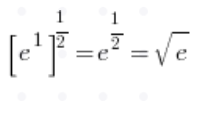
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
Mam do Pana pytanie odnośnie powyższego wzoru na liczbę e, czy w miejscu litery “a” może być cyfra inna niż 1, ponieważ na ostatni konsultacjach po kolokwium, mój profesor stwierdził, że wzór ten jest prawdziwym i można go stosować tylko i wyłącznie wtedy gry w miejscu litery “a” ( we wzorze powyżej) znajduje się cyfra 1 i żadna inna. Argumen\tował to tak, że twierdzenie wyraźnie mówi o wzorze (1+1/n)^n=e , a twierdzenia z innymi cyframi nie ma, więc aby zastosować ten wzór należy tak przekształcać granicę aż osiągniemy tę postać i wszystkie wyniki, w których w liczniku była liczba inna niż 1 przekreślał i obcinał punkty.
Jest wzór na to. Wynik wyjdzie “e”. Oczywiście przy lim ->0.
Witam.
Mam pewien problem dotyczacy metody obliczania pewnych granic ciagow ze wzoru na liczbe e. Uczylem sie Twojego sposobu czyli tego wzoru na gorze “wzor na liczbe e z definicji”.
Tylko jest jeden problem poniewaz w niektorych przypadkach na ćw. dostalem ochrzan ze w zadnym wypadku nie moge stosowac takiej metody bo jest bleda. Mam na mysli przyklady gdzie pod wspolczynnikiem ‘a’ z tego wzoru kryje sie np “2n+2”. Czyli mamy np lim[(1+ ((2n+2)/(n-1)) ]^n+1 Wg Twojej metody nalezalo zrobic odwrotnosc ((2n+2)/(n-1))zeby bylo 1/((n-1)/(2n+2)) no i dalej bez problemu liczyc(sam tak licze od dluzszego czasu i wychodza dobre wyniki). No i w tym pojawil sie problem bo pani profesor powiedziala ze absolutnie nie mozna tak robic bo to zmienia postac granicy czy cos w tym rodzaju. Glownie chodzilo o to ze wg podstawowego wzoru na liczbe e lim(1+an)^(1/an)=e an musi dazyc do 0 a po przeksztalceniach ten warunek nie jest zachowany
Sam juz niewiem jak takie przyklady robic bo niby wynik jest dobry no ale na kolokwium nie chcialbym zeby mi profesorka dala 0 pkt “bo ona mowi tak sie nie da tego liczyc” 😉
Pozdrawiam.
Dzięki za pytanie, jeżeli chodzi o Twój przykład:
lim[pmath](1+{2n+2}/{n-1})^{n+1}[/pmath]
To oczywiście, że mojej |metody” nie można zastosować, bo wyrażenie [pmath]{2n+2}/{n-1}[/pmath] nie dąży do 0, tylko do 2, czyli wyrażenie w nawiasie do 3, czyli mamy 3 do nieskończoności, czyli w ogóle nie mamy symbolu nieoznaczonego!
Dalej: wyrażenie ‘an’ również NIGDY nie będzie dążyć do 0 przy n dążącym do nieskończoności 🙂
Twoje wyrażenie:
lim[pmath](1+an)^{1/{an}}[/pmath]
to symbol nieoznaczony [pmath]{\infty}^0[/pmath] – i w nim nie stosujemy raczej w ogóle przekształceń do wzoru na liczbę e.
Polecił bym raczej de’Hospitala.
O ile dobrze Cię zrozumiałem, oczywiście…
faktycznie może troche zły przykład.
Z tego co pamiętam to właśnie przy robieniu tego przykładu co jest w linku zostalem pouczony, że absolutnie nie mogę takiej metody stosować. Z tego co zrozumiałem to pani profesor mówiła ogólnie o przykładach w których w nawiasie robi sie odwrotność tego jednego składnika.
Wszystkie tego typu zadania robię od dluzszego czasu taka metodą i zawsze wyniki wychodzą dobre.
Jeśli chodzi o Pana przykład, to niestety nie bardzo rozumiem, dlaczego nie można zastosować “mojej” metody.
Wyrażenie: [pmath]{3n-1}/{n^2-2n-2}[/pmath] zbiega do 0.
Po “moim” przekształceniu wyrażenie: [pmath]1/{{n^2-2n-2}/{3n-1}}[/pmath] NADAL zbiega do 0.
Nie dało by się podejść do Pani Profesor i poprosić o dokładne wytłumaczenie, dlaczego “nie można” ?
Z tego co się orientuję, do sesji daleko i profesorzy są teraz o wiele bardziej – że tak powiem – “przystępni” w godzinach konsultacji 🙂
Nie bardzo rozumiem” Najpierw wypadało by wykazać, że wyrażenie [pmath]sqrt{n+1}-\sqrt{n}[/pmath] dąży do zera. Zrobisz to, licząc granicę:
[pmath]{lim}under{n{right}{\infty}}(sqrt{n+1}-\sqrt{n})[/pmath] – wyjdzie faktycznie równa zero.”dlaczego ona zbiega do 0 jak wychodzi mi wynik nieskończoność minus nieskończoność w nawiasie bo pierwiastkujemy nieskończoność??
Nieskończoność minus nieskończoność to nie wynik, tylko symbol nieoznaczony.
Należy zastosować metodę mnożenia przez sprzężenie:
[pmath]{lim}under{n{right}{\infty}}(sqrt{n+1}-\sqrt{n})={lim}under{n{right}{\infty}}(sqrt{n+1}-\sqrt{n}){\sqrt{n+1}+\sqrt{n}}/{\sqrt{n+1}+\sqrt{n}}=[/pmath]
[pmath]{lim}under{n{right}{\infty}}{n+1-n}/{\sqrt{n+1}+\sqrt{n}}={lim}under{n{right}{\infty}}1/{\sqrt{n+1}+\sqrt{n}}=0[/pmath]
Nie prościej podzielić wszystko przez n^2?
“… która po zastosowaniu mnożenia przez sprzężenie zakończy się wynikiem 1.”
Zakończy się wynikiem 1/2 … -_-
Racja, dzięki za czujność i pomoc. Poprawiłem.