Bestimmte Integrale können sowohl bezüglich der Variablen x als auch y berechnet werden, und manchmal sollte das auch geschehen, wenn es bequemer ist. Dies spielt oft eine große Rolle bei der Anwendung von Integralen, wie z.B.: Berechnung der Flächen von Regionen, Bogenlängen, Volumen und Oberflächenbereiche von Rotationskörpern. Oft haben wir nicht einmal eine Wahl, da die Bedingungen der Aufgabe festlegen, dass sich die Kurve um die OY-Achse und nicht um die OX dreht.
Wie macht man das?
Zuerst musst du eine Zeichnung anfertigen und darauf das Gebiet/die Bogenlänge/das Volumen markieren, das berechnet werden soll. Ohne das geht es nicht los.
Zweitens musst du die Integrationsgrenzen auf der OY-Achse bestimmen (ähnlich wie auf der OX-Achse).
Nun musst du nur noch die begrenzenden Kurven für die Daten (üblicherweise) bezüglich der Variablen x unter Verwendung der Variablen y bestimmen, zum Beispiel haben wir die Kurve ![]() , wir bestimmen „x“ und erhalten so zwei Funktionen der Variablen y:
, wir bestimmen „x“ und erhalten so zwei Funktionen der Variablen y: 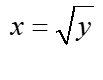 und
und 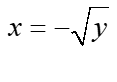 .
.
Dann erstellen wir einfach das entsprechende Integral mit Integrationsgrenzen auf der OY-Achse und Funktionen der Variablen y, zum Beispiel im Bereich der Fläche wäre es:
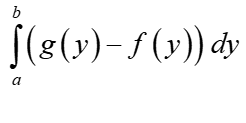
Ich wiederhole noch einmal, die Grundlage ist ein klares, großes Diagramm!


