Hinreichende Bedingung für die Existenz eines Extremums einer Funktion

Extrema von Funktionen Vorlesung 7

Thema: Hinreichende Bedingung für das Vorhandensein eines Extremums einer Funktion (Zeichenwechsel der Ableitung).

Zusammenfassung

Wie sich in der vorherigen Vorlesung herausstellte, bedeutet die Tatsache, dass die Ableitung einer Funktion an einem Punkt gleich 0 ist, nicht notwendigerweise, dass die Funktion an diesem Punkt ein Extremum erreicht. Hier werden wir also besprechen, welche Bedingungen ausreichen, damit eine Funktion an einem Punkt ein Extremum erreicht.

Hinreichende Bedingungen für das Vorhandensein eines Extremums

Angenommen, in einer Umgebung des Punktes $x_0$ hat die Funktion $f \left(x \right)$ eine endliche Ableitung $f' \left( x \right)$ :

Wenn in dieser Umgebung von $x_0$ links von $x_0$ die Werte der Ableitung der Funktion positiv sind und rechts von $x_0$ negativ – dann nimmt die Funktion ein Maximum im Punkt $x_0$ an
Wenn in dieser Umgebung von $x_0$ links von $x_0$ die Werte der Ableitung der Funktion negativ sind und rechts von $x_0$ positiv – dann nimmt die Funktion ein Minimum im Punkt $x_0$ an

Tatsächlich, gemäß dem in der vorherigen Vorlesung eingeführten Lemma über die Monotonie von Funktionen, wenn die Ableitung der Funktion positive Werte annimmt, bedeutet dies, dass die Funktion steigend ist. Wenn jedoch die Ableitung negative Werte annimmt, bedeutet dies, dass die Funktion fallend ist.

Wenn also die Ableitung “ihr Zeichen wechselt”, bedeutet dies auch eine Änderung der Monotonie der Funktion , zum Beispiel im Fall 1:

Die Ableitung links von ist positiv, und rechts negativ. Das bedeutet, dass die Funktion links von steigt und rechts fällt. Es muss also irgendwie so aussehen: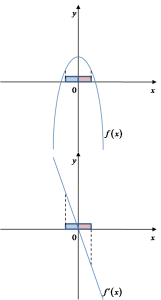
Im obigen Diagramm haben wir das Diagramm der Funktion (oben) und ihrer Ableitung . Man sieht, dass in der “linken” Umgebung des Punktes (blau markiert) die Ableitung positive Werte annimmt und die Funktion steigt. In der “rechten” Umgebung des Punktes (rot markiert) nimmt die Ableitung negative Werte an und die Funktion fällt.