Sufficient condition for the existence of a function's extremum

Function Extrema Lecture 7

Topic: Sufficient condition for the existence of a function’s extremum (change in the sign of the derivative).

Summary

As we found out in the previous Lecture, just because the function’s derivative at a point is equal to 0 doesn’t necessarily mean that the function itself reaches an extremum at that point. So, here we’re going to talk about what conditions are sufficient for a function to reach an extremum at some point.

Sufficient Conditions for the Existence of an Extremum

Assume that in some neighborhood of the point $x_0$ , the function $f \left(x \right)$ has a finite derivative $f' \left( x \right)$ :

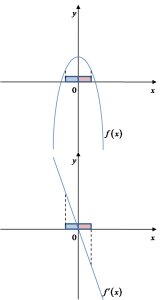
If in this neighborhood of $x_0$ , to the left of $x_0$ , the values of the function’s derivative are positive, and to the right of $x_0$ negative – then the function assumes a maximum at the point $x_0$
If in this neighborhood of $x_0$ , to the left of $x_0$ , the values of the function’s derivative are negative, and to the right of $x_0$ positive – then the function assumes a minimum at the point $x_0$

Indeed, according to the Lemma on the Monotonicity of Functions introduced in the previous Lecture, if the function’s derivative takes positive values, it means that the function is increasing. If, however, the derivative takes negative values, it means that the function is decreasing.

If, therefore, the derivative “changes sign”, it also indicates a change in the monotonicity of the function , for example in case 1:

The derivative to the left of is positive, and to the right negative. This means that the function to the left of is increasing, and to the right decreasing. It must look something like this:
In the graph above, we have the graph of the function (at the top) and its derivative . It can be seen that in the “left” vicinity of the point (marked in blue) the derivative takes positive values, and the function is increasing. In the “right” vicinity of the point (marked in red) the derivative takes negative values, and the function is decreasing.