Warunek dostateczny istnienia ekstremum funkcji

Ekstrema Funkcji Wykład 7

Temat: Warunek dostateczny istnienia ekstremum funkcji (zmiana znaku pochodnej).

Streszczenie

Jak okazało się na poprzednim Wykładzie, samo to, że pochodna funkcji w punkcie równa jest 0 nie musi oznaczać, że sama funkcja osiąga w tym punkcie ekstremum. Tutaj powiemy więc sobie, jakie warunki wystarczą, aby funkcja osiągała w jakimś punkcie ekstremum.

Warunki wystarczające istnienia ekstremum

Załóżmy, że w pewnym otoczeniu punktu $x_0$ funkcja $f \left(x \right)$ posiada pochodną skończoną $f' \left( x \right)$ :

Jeżeli w tym otoczeniu $x_0$ na lewo od $x_0$ wartości pochodnej funkcji są dodatnie, a na prawo od $x_0$ ujemne – wtedy funkcja przyjmuje maksimum w punkcie $x_0$
Jeżeli w tym otoczeniu $x_0$ na lewo od $x_0$ wartości pochodnej funkcji są ujemne, a na prawo od $x_0$ dodatnie – wtedy funkcja przyjmuje minimum w punkcie $x_0$

Istotnie, zgodnie z wprowadzonym na poprzednim Wykładzie Lematem o Monotoniczności Funkcji zmiana jeżeli pochodna funkcji przyjmuje wartości dodatnie, oznacza to, że funkcja jest rosnąca. Jeżeli zaś pochodna przyjmuje wartości ujemne, to znaczy, że funkcja jest malejąca.

Jeżeli więc pochodna “zmienia znak”, to oznacza też zmianę monotoniczności funkcji , na przykład w przypadku 1.:

Pochodna na lewo od jest dodatnia, a na prawo ujemna. Oznacza to, że funkcja na lewo od rośnie, a na prawo maleje. Musi to wyglądać więc jakoś tak:
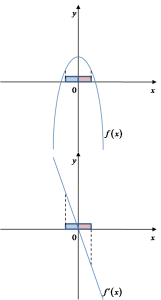Na wykresie wyżej mamy wykres funkcji (u góry) i jej pochodnej . Widać, że w “lewym” otoczeniu punktu (zaznaczonym na niebiesko) pochodna przyjmuje wartości dodatnie, a funkcja jest rosnąca. W “prawym” otoczeniu punktu (zaznaczonym na czerwono) pochodna przyjmuje wartości ujemne, a funkcja jest malejąca.