Rozwiązania z oficjalnej matury z matematyki CKE – MAJ 2019 – poziom PODSTAWOWY. Dodatkowo rozwiązanie każdego z zadań w formie obrazka.
Kurs Maturalny z matematyki poziom rozszerzony! Jest to Kurs typowo z zadaniami maturalnymi. Dotyczy tematów: funkcje, rachunek różniczkowy, ciągi i trygonometria. Każda lekcja zawiera zadania zamknięte testowe, zadania kodowane oraz otwarte (łącznie po 30 zadań do każdej z Lekcji). Dodatkowo otrzymujesz porcję zadań „na rozgrzewkę”, jako małe przypomnienie materiału.
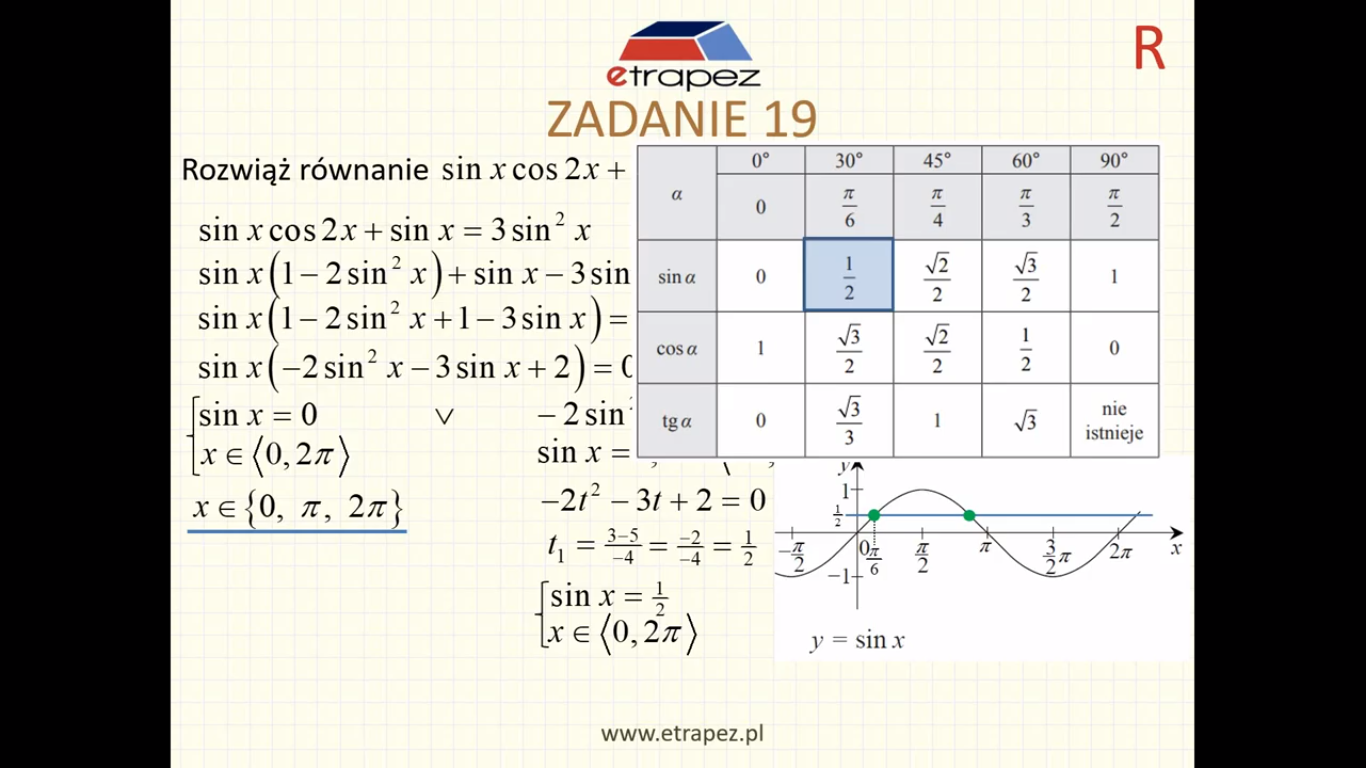
Fragment Lekcji NOWEGO Kursu Matura rozszerzona cz.2. Lekcja nr 8 – Trygonometria.
Na tym filmiku pokazuję jak się zabrać za równanie trygonometryczne, tak od początku. Ważne są dwie kwestie: by mieć te same kąty oraz by mieć jak najmniej „rożnych” funkcji. Zobacz jak tłumaczę rozwiązywanie tego typu równań. I jak łatwo odczytać wszystkie potrzebne wartości z wykresu, zamiast kuć na pamięć np. redukcyjne.
Oto fragment kolejnej – trzeciej lekcji dotyczącej ciągów NOWEGO, tworzącego się Kursu eTrapez skierowanego do maturzystów z matematyki – Matura Rozszerzona część 2. Zadanie: „Trzy liczby, których suma jest równa 65, tworzą ciąg geometryczny. Liczby te są jednocześnie pierwszym, trzecim i dziewiątym wyrazem pewnego ciągu arytmetycznego. Wyznacz te liczby.”
Zadanie polecane również maturzystom z zakresu PODSTAWOWEGO – podobnego typu zadanie zdarza się często na maturze majowej jako zadanie otwarte. 🙂
Chcesz zdać maturę? Matematyka w szkole średniej Cię przeraża? Bądź z nami w KAŻDĄ ŚRODĘ o godz 18:00 na naszym kanale na YouTube! START: 27. lutego (środa), godz 18:00.
Będzie to cykl spotkań na żywo MATURA Z ETRAPEZEM „Matematyka Jest Prosta”, z dwiema osobami z ekipy eTrapez. Weźmiemy na warsztat jedno wybrane zagadnienie z matematyki – pewniak maturalny – i omówimy je dokładnie na kilku zadaniach wprost z arkuszy maturalnych. Krótko, zwięźle i na temat.
Wirtualny nauczyciel AI działający w przeglądarce internetowej.