
Podstawienia Eulera I rodzaju
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Podstawienia Eulera – komu to potrzebne?
Podstawienia Eulera w całkach nieoznaczonych są następną rzeczą, którą wprowadza się po całkach wymiernych, całkach trygonometrycznych i całkach z pierwiastkami (albo według niektórych klasyfikacji: “całkach niewymiernych”). Co oznacza, że większość studentów nie będzie miała przyjemności się z nimi spotkać, nie ująłem ich także w moim Kursie Całek Nieoznaczonych .
Pozostaje jednak całkiem spora grupa studentów na kierunkach matematycznych, albo naprawdę, naprawdę “mocnych” matematycznie, którzy z podstawieniami Eulera muszą się zmierzyć i tych (a także ciekawych) zapraszam. Omówię wszystkie trzy rodzaje podstawień Eulera (w tym poście wezmę się za I rodzaj) i do każdego zrobię po jednym przykładzie.
Jedziemy.
Jakie całki rozwiązujemy podstawieniami Eulera?
Podstawieniami Eulera rozwalamy całki typu:

…czyli jakieś dowolne związki ![]() i
i ![]() . Można je więc potraktować jako pewne “przedłużenie” tematu całek z pierwiastkami (“niewymiernych”).
. Można je więc potraktować jako pewne “przedłużenie” tematu całek z pierwiastkami (“niewymiernych”).
Podstawieniami Eulera rozwalamy całki, których nie da się rozwiązać prościej, oczywiście. Na przykład całka:
![]() to jest całka, w której mamy związek
to jest całka, w której mamy związek ![]() i
i ![]() , ale można ją rozwiązać bardzo prosto przez głupie podstawienie:
, ale można ją rozwiązać bardzo prosto przez głupie podstawienie: ![]() . Nie strzelamy więc z armaty do wróbla i w takich prostych całkach nie męczymy się Eulerem.
. Nie strzelamy więc z armaty do wróbla i w takich prostych całkach nie męczymy się Eulerem.
Weźmy jednak całkę:
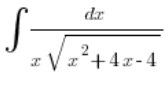
Widzimy, że sytuacja jest poważniejsza, sprawy nie rozwiążą nam znane wcześniej podstawienia ![]() , czy
, czy ![]() (nie wyznaczymy z nich
(nie wyznaczymy z nich ![]() ).
).
Potrzebujemy nowej broni.
Podstawienia Eulera – I rodzaj
Mając całkę:

w której ![]() ,
,
stosujemy podstawienie:
![]()
, podnosimy obie strony do kwadratu, składniki ![]() się skracają (i o to chodzi), wyznaczamy (w kolejności):
się skracają (i o to chodzi), wyznaczamy (w kolejności):
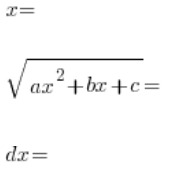
, wyrażone związkami t, podstawiamy do całki wyjściowej:

i mamy całkę zmiennej t (jeśli ostały nam się w niej jakieś x-sy, to popełniliśmy błąd) i jest to całka wymierna.
Uwaga
Warto jeszcze dodać, że w praktyce wielu studentów ma wprowadzone podstawienia Eulera tylko I rodzaju i tylko do całek typu:

, czyli takich, w których jakby ![]()
Prześledźmy podstawienia Eulera I rodzaju w akcji, na przykładzie:
Przykład 1
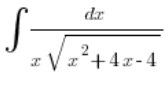
Stwierdzamy, że jest to całka, w której jest związek ![]() i
i ![]() . Że nie da się rozwiązać ją prosto. Że
. Że nie da się rozwiązać ją prosto. Że ![]() (
(![]() to oczywiście współczynnik przy
to oczywiście współczynnik przy ![]() , w naszym przykładzie jest on równy 1).
, w naszym przykładzie jest on równy 1).
Czyli brykać będziemy podstawieniem Eulera I rodzaju.
Podstawiam:
![]()
czyli po prostu:
![]()
podnoszę obie strony do kwadratu:
![]()
Składniki z ![]() po obu stronach się skracają (i tak ma właśnie być za każdym razem):
po obu stronach się skracają (i tak ma właśnie być za każdym razem):
![]()
No i teraz właśnie trzeba wyznaczyć ![]() ,
, ![]() i
i ![]() (w tej kolejności).
(w tej kolejności).
Zaczniemy od ![]() :
:
![]()
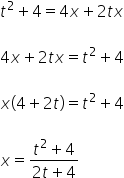
Mamy ![]() wyrażone zmienną t. Teraz kolej na
wyrażone zmienną t. Teraz kolej na ![]() , czyli w naszym przykładzie:
, czyli w naszym przykładzie: ![]() .
.
Wracamy się do naszego pierwszego podstawienia, w którym było:
![]()
Teraz znamy już ![]() (widać, dlaczego ważna jest kolejność, prawda?), możemy więc napisać:
(widać, dlaczego ważna jest kolejność, prawda?), możemy więc napisać:
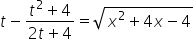
czyli:
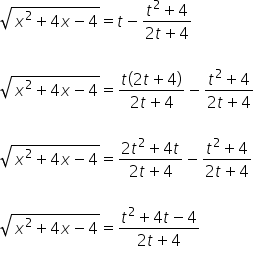
Mamy więc ![]() wyrażone zmienną
wyrażone zmienną ![]() .
.
Na koniec ![]() , które bierzemy już po prostu różniczkując obie strony wyznaczonego
, które bierzemy już po prostu różniczkując obie strony wyznaczonego ![]() :
:
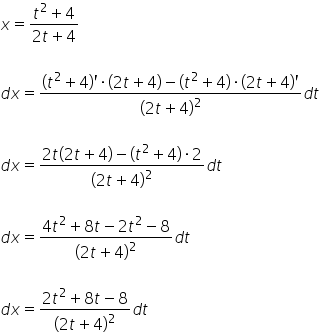
I w ten sposób wyznaczamy ![]() . Mamy więc:
. Mamy więc:
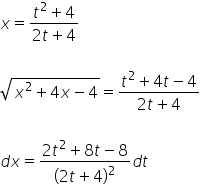
Wstawiamy to wszystko do całki wyjściowej:
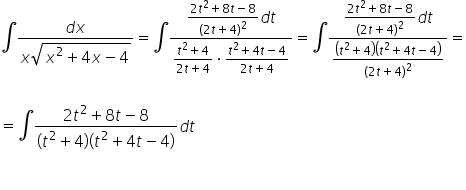
Na pierwszy rzut oka wygląda nam to na nudną, żmudną, ale już znana i schematyczna całka wymierna (rozkład na ułamki proste, drugi czynnik w mianowniku da się jeszcze bardziej rozłożyć). Na ogół tak jest, ale w tym konkretnym przykładzie będziemy mieli trochę szczęścia i przebijanie się przez 3 strony a4 obliczeń zostanie nam oszczędzone:
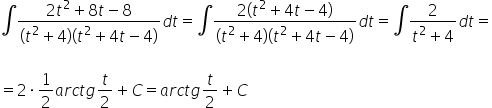
Jak wrócić się podstawieniem? Mieliśmy na początku:
![]()
Stąd oczywiście:
![]()
Czyli nasz wynik to:
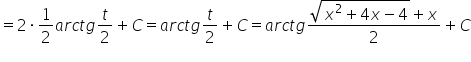
CDN. (mamy jeszcze dwa rodzaje podstawień Eulera, co jeśli współczynnik ![]() nie jest większy od zera?).
nie jest większy od zera?).
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.










mam nadzieję że zarabia pan na swojej działalności kupę kasy, bo naprawdę pomaga pan masie osób
Ale to podstawienie nie jest głupie ;-;
Jak policzyć taką całkę:
Integral(1/[x+(x^2+x+1)^1/2])dx
Mógłbyś napisać coś o \interpretacji geometrycznej tych podstawień
chociażby na wypadek gdyby ktoś je zapomniał
Spotkałam się z takim zapisem podstawienia Eulera I rodzaju: [/latex]sqrt{ax^{2}+bx+c}=\pm [/latex]sqrt{a}+t
Kiedy używamy „+” a kiedy „-„?
[/latex]sqrt{ax^{2}+bx+c}=\pm[/latex]sqrt{a}x+t
Nie wiem dlaczego nie wyświetla się poprawnie :/
Całki postaci \int{Rleft(x,sqrt{ax^2+bx+c}mbox{d}x}
można przedstawic jako sumę trzech całek \int{R_{1}\left(xright)mbox{d}x}+\int{R_{2}\left(sqrt{ax^2+bx+c}right)mbox{d}\sqrt{ax^2+bx+c}}+\int{R_{3}{\left(frac{x+\frac{b}{2a}}{\sqrt{ax^2+bx+c}}right)}mbox{d}\frac{x+\frac{b}{2a}}{\sqrt{ax^2+bx+c}}}
Podobno można tego dokonac drogą algebraiczną
Witam. Zbiór elementarnych kursów, które są realizowane na każdej uczelni, już zagościł w tym serwisie:) Zostało prawdopodobieństwo, statystyka ale z tym jest różnie na uczelniach. Ja miałem jeszcze na koniec ostatniego semestru (kier. energetyka) takie zagadnienia jak: funkcje zespole, całki funkcji zespolonych, badanie holomorficzności funkcji. Kursy można oczywiście rozszerzać. Wszystko zależy od chęci Pana Krystiana. Może w przyszłości jakiś podstawowy kurs z 3DGrapher’a albo MATLABA? Pozdrawiam
Ja proponuje prawdopodobieństwo jest na każdym profilu studiów matematycznych a statystyka nie
krystian, dawaj na pg flache obalic!
Super są te Pana kursy:) Można zapytać czy ma Pan w planie jeszcze jakieś kursy? A jeśli tak, to jaki temat będzie obejmował następny :)?
Pozdrawiam,
Ania
Dzięki 🙂 Tak, będę tworzył następ\ne Kursy. Co do następ\nego myślałem o Statystyce, ale można najpierw zrobię Prawdopodobieństwo, nie zdecydowałem się jeszcze…
Fajne, więcej takich. Dzięki.