W całeczkach bez wzorów ani rusz. Zamieszczam więc PDFy z odpowiednimi wzorami, uzbrojony w które możesz podjąć walkę z jakimś tam momentem bezwładności stożka, albo polem powierzchni kuli wykrojonej walcem.
Na początku to, co powinieneś już UMIEĆ, podchodząc do całek wielokrotnych. Nie chodzi mi o to, że powinieneś umieć te wszystkie wzory na pamięć, tylko o to, że takie np. całki nieoznaczone musisz już umieć liczyć.
Tabela podstawowych wartości trygonometrycznych
Teraz zaczynamy od całek podwójnych, przejścia na współrzędne biegunowe, ich zastosowań itd. Dodałem też zastosowania fizyczne całek podwójnych:
Co do całek potrójnych mamy współrzędne sferyczne i walcowe i oczywiście zastosowania fizyczne:
Całki krzywoliniowe wyglądają groźnie, ale jak już się się zna wzór na przejście na całkę oznaczoną…
Całki powierzchniowe to już naprawdę ostra jazda, ale ogólnie w teorii chodzi tylko o to, żeby przejść na podwójną (zdecydowanie polecam współrzędne parametryczne, jak we wzorach), albo potrójną (Gaussem-Ostrogradskiem, także we wzorach):
Na deserek już tylko porcja wzorów do pól wektorowych:
Oczywiście nie nastawiaj się, że same wydrukowanie sobie tych wzorów pomoże, gdyby to było łatwe, w ogóle żadne szkoły nie były by potrzebne. Jak ich używać możesz dowiedzieć się na przykład w moim Kursie. Ale mam nadzieję, że się przydadzą. Warto je mieć skondensowane, wyselekcjonowane (wykreślaj sobie to, czego nie potrzebujesz, to ważne) i pod ręką 🙂

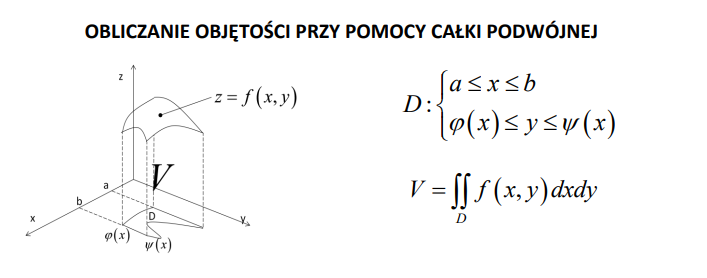

25 Komentarzy
Tomasz
Zastanawia mnie w jaki sposób można obliczyć całki n-krotne? Na przykład jeśli mamy do obliczenia całkę cztero czy pięciokrotną?
Krystian Karczyński
To dosyć proste. Żeby policzyć np. całkę „poczwórną” po x,y,z,t można policzyć całkę po zmiennej x w jej granicach całkowania. Pozostałe, czyli y,z,t traktujemy jako stałe. Wynik jest funkcją zmiennych y,z,t. Potem z tej funkcji liczymy całkę po zmiennej np. y (po granicach całkowania y). Wynik jest funkcją zmiennych z i t. Z wyniku liczymy całkę np. po z. Wynik jest funkcją zmiennej t. Z wyniku liczymy całkę po t i mamy wynik jako liczbę.
Całki poczwórne i dalej jednak – z tego co wiem – nie mają na dzisiaj praktycznego zastosowania, dlatego kończymy edukację na potrójnych.
Piotr
Linki nie działają.
Krystian Karczyński
Poprawiłem, dzięki, przepraszam.
Klara
Witam, mam problem z przejściem na współrzędne sferyczne. Znam wzory, ale nie wiem w jakich granicach po zamianie powinny się znajdować ro,fi i teta
Magda
Mam pytanie odnośnie objętości bryły liczonej całką podwójną. Mam obliczyć bryły ograniczonej z=x^2+y^2, z=4. czy rzut na OXY będzie r oraz fi, i czy wzór będzie calka z (4-r^3) czy tylko r^3 ?
Anna Zalewska
adrian
Witam, nie mam pojecia jak zabrać sie do tego zadania proszę o pomoc
całka potrójna
Obliczyć masę kostki o długości krawędzi równej 2, jeżeli gęstość w każdym punkcie równa jest
odległości punktu od podstawy kostki.
Anna Zalewska
Paweł
dzięki
Paweł
Nie podziękowałem za dotychczasową pomoc, dziękuje… teraz wrzucę skan kartki z egzaminu w nim jest zadania z ćwiartką koła i teraz przynajmniej nie pomylę się… http://zapodaj.net/9e61effc401f8.jpg.html jeszcze drobna prośba. Oglądałem ostatnio trochę filmów z etrapez i ciekawi mnie jak zabrać się za zadania z egz za wyjątkiem 3, które jest banalne(skan), w przypadku pierwszego zadania wiem, że to będzie parabolka ograniczona od 0 do pierwiastek z 3… i mniej więcej ogarniam, najwięcej osób u nas na ATH w bielsku poległo na zad od 3 do 5 sam nie wiem jak dokonca też w sumie nie wiem jak za to się zabrać dlatego proszę o pomoc
Krystian Karczyński
No to jeżeli chodzi o tą ćwiartkę koła to jest powiedziane, że jest ona JEDNORODNA, przyjmuję więc za \rho =1i podstawiam tylko do odpowiednich wzorów na całki podwójne:
Najpierw masa M:
M=\iint\limits_{D}{\rho \left( x,y \right)dxdx}=\iint\limits_{D}{dxdy}
Żeby policzyć tą całkę korzystam z pewnego patentu, opisanego w moim Kursie . Wiem, że całka podwójna z samego dxdy, „bez” funkcji podcałkowej z jakiegoś obszaru równa jest POLU tego obszaru (czyli ćwiartce koła), zatem:
M=\iint\limits_{D}{dxdy}=\frac{1}{4}\cdot \pi \cdot {{1}^{2}}=\frac{1}{4}pi
Liczę momenty statyczne z wzorów:
{{M}_{x}}=\iint\limits_{D}{ydxdy}
{{M}_{y}}=\iint\limits_{D}{xdxdy}
Oczywiście ze względu na obszar całkowania przechodzę na współrzędne biegunowe: x=r cos \varphi , y=r sin \varphi , gdzie:
\{ \begin{matrix}
&0\le r\le 1 \\
&0\le \varphi \le \frac{\pi }{2}
\end{matrix}
Czyli mam:
{M}_{x}=\iint\limits_{D}{ydxdy}=\int\limits_{0}^{1}{{ \int\limits_{0}^{\frac{\pi }{2}}{sin \varphi d\varphi } }rdr}=\ldots =\frac{1}{2}
{{M}_{y}}=\iint\limits_{D}{xdxdy}=\int\limits_{0}^{1}{{ \int\limits_{0}^{\frac{\pi }{2}}{cos \varphi d\varphi } }rdr}=\ldots =\frac{1}{2}
Czyli współrzędne środka ciężkości to:
\left( \frac{\tfrac{1}{2}}{\tfrac{\pi }{4}},\frac{\tfrac{1}{2}}{\tfrac{\pi }{4}} \right)=\left( \frac{2}{\pi },\frac{2}{\pi } \right)
Paweł
Witam jak zabrać się za zadania takiej treści: 1. Wyznaczyć środek ciężkości jednorodnej ćwiartki koła x^2+y^2=0; y=>0
2. Powołując się na znane zastosowanie całek krzywoliniowych obliczyć całkę krzywoliniową nieskierowaną całka z L (2x-y)dl gdzie L jest okręgiem x^2+y^2=<1. Uwaga rozwiązania bezpośrednie nie będą brane pod uwagę. Z góry dziękuje za każdą pomoc
Krystian Karczyński
Witam,
1. Coś chyba nie tak, {{x}^{2}}+{{y}^{2}}=0to NIE jest równanie okręgu (po prawej jest zero, czyli promień by musiał być równy 0…), ani nawet ćwiartki okręgu (dla y\ge 0była by to połówka okręgu, zakładając, że miał by jakiś promień).
2. Nie wiem, o jakie „znane” zastosowanie chodzi, sorry… Licząc tą całkę normalnie (nie przez to nieznane mi znane zastosowanie 🙂 ) zapisalibyśmy ten okrąg w postaci parametrycznej:
\{ \begin{matrix}
&x=cost\\
&y=sint\end{matrix} , t \in \left\langle {0,2\pi } \right\rangle
i podstawili po prostu do wzoru na całkę krzywoliniową nieskierowaną:
\int\limits_{L}{\left( 2x-y \right)dL}=\int\limits_{0}^{2\pi }{\left( 2cos t-sin t \right)\sqrt{{{\left( -sin t \right)}^{2}}+{{\left( cos t \right)}^{2}}}dt}=\int\limits_{0}^{2\pi }{\left( 2cos t-sin t \right)\sqrt{{{sin }^{2}}t+{{cos }^{2}}t}dt}=
=\int\limits_{0}^{2\pi }{\left( 2cos t-sin t \right)dt}=\ldots =0
No i pewno (sądząc po poleceniu) jakoś można od razu było stwierdzić, że wyjdzie to zero, ale nie wiem jak… Ale jak by ktoś wiedział, to byłbym wdzięczny za komentarz.
Paweł
W przypadku profesora chodzi mu o znane zastosowania czyli po prostu w oparciu o definicje, i pomyłka z tym kołem wiem nie może być 0 tylko ma być 1 ale to było pisane nie przemyślanie
mat
sorry moj błąd
Rafał
Witam!
Mam problem ze ściągnięciem instalki do kursu: ” Kurs Całki Wielokrotne”
Bardzo bym prosił o przesłanie mi aktualnego linka na maila.
Z góry dziękuje!
Podane niżej linki nie działają:
mat
zadanie 1 przyklad 1 w zestawie zadania domowego w odpowiedziach jest 1/3 , wydaje mi sie ze powinno byc 5/6
Paweł
Dziękuje za pomoc:)
Paweł
Witam:) mam taki problem:) Jak wyprowadzić wzór na objętośc ostrosłupa prawidłowego
o wysokości 2H i podstawie kwadratowej o przekątnej 2a stosując rachunek całkowy?:)
Bardzo będę wdzięczny za pomoc:)
Krystian Karczyński
Witam! To bardzo fajne pytanie i chciałem na nie odpowiedzieć postem na blogu, ale niestety zrobił mi się kocioł w pracy i w najbliższym czasie nie dam rady.
No ale tak w skrócie – rysujemy i liczymy 🙂 a,H – traktujemy jak stałe, liczby.
1. Rysujemy ostrosłupka tak, żeby wysokość miał na osi Oz, a przekątne na osiach Ox, Oy.
2. Zadanie jest przyjaźnie ułożone, liczymy objętość ćwiartki ostrosłupa i mnożymy przez 4. Powierzchnia ograniczająca bryłę z góry to ściana ostrosłupa – jej równanie to [pmath]x/a+y/a+z/{2H}=1[/pmath] – tylko „z” trzeba wyznaczyć. Wziełem to sobie z równania odcinkowego płaszczyzny.
Obszar całkowania to 0 do x do a i 0 do y do -x+a (narysować w dwóch wymiarach i wyznaczyć równanie prostej).
3. Liczymy całkę podwójną w tych granicach z funkcji „z” i mnożymy przez 4 i mamy wynik jakiś z a i H na pewno.
Dawid
Czy jest mozliwość dostatania tylko jednej lekcji chodzi mi o Lekcje 1- Całki podwójne
Krystian Karczyński
Nie, nie ma takiej możliwości, przykro mi…
klimczyk
nie da się otworzyć karty z poszczególnymi wzorami
Krystian Karczyński
Poprawiłem linki, przepraszam.