Kalkulator do dziedziny

Krystian Karczyński

Przedstawiam kolejny z „moich” kalkulatorów, tym razem wyznaczający dziedzinę funkcji:

Warto zauważyć, że kalkulator wyznaczy także (a przynajmniej się postara) dziedzinę funkcji wielu zmiennych .

Zapraszam zatem do sprawdzania dziedzin (funkcje wpisujemy zgodnie z ogólną instrukcją wpisywania formuł matematycznych).

Poniżej lista innych moich kalkulatorów na blogu:

Kalkulator do pochodnych cząstkowych

Kalkulator do pochodnych

Kalkulator do całek nieoznaczonych

Kalkulator do całek podwójnych

Kalkulator do całek potrójnych

Kalkulator do równań różniczkowych

Kalkulator do szeregów

konometria jest dosyć młodą dziedziną wypływającą z ekonomii i matematyki. W praktyce, dzięki modelom ekonometrycznym, możesz „zmierzyć gospodarkę”.Polega to konkretnie na zmierzeniu, jak zachowuje się jedna zmienna w zależności od innych. I na podstawie analizy tego, co było, możesz określać, co będzie się działo w przyszłości.

Wykorzystasz do tego przeróżne obliczenia, testy, schematy. Jedne będą bardzo proste, inne trudniejsze. Jednak najczęściej będzie się liczyło nie to, jak dojdziesz do wyniku, ale jak go zinterpretujesz, odczytasz i jakie wnioski wyciągniesz.

Poniższe Wykłady dotykają najważniejszych pojęć teoretycznych. Jestem przekonana, że pomogę Ci odkrywaniu tego, czym jest ekonometria. I przy okazji uda Ci się zaliczyć ten przedmiot na studiach.

15 Komentarzy

Jezus
11 kwietnia 2022 at 17:20

Witam potrzebuje pomocy jak wykonac takie zadanie

x-4/x³-3x

Odpowiedz
1. Krystian Karczyński
  14 kwietnia 2022 at 14:53
  
  Chodzi o wyznaczenie dziedziny funkcji $\frac{{x – 4}}{{{x^3} – 3x}}$ , prawda?
  
  Nie można dzielić przez zero, czyli trzeba policzyć, kiedy:
  
  ${x^3} – 3x = 0$
  
  No to liczę:
  
  $x\left( {{x^2} – 3} \right) = 0$
  
  $x\left( {x – \sqrt 3 } \right)\left( {x + \sqrt 3 } \right) = 0$
  
  $x = 0 \vee x = – \sqrt 3 \vee x = \sqrt 3$
  
  Dla tych wartości $x$ mianownik jest równy zero. A że nie może właśnie być równy zero, mamy w ten sposób wyznaczoną dziedzinę:
  
  $Df:x \in \backslash \left\{ { – \sqrt 3 ,0,\sqrt 3 } \right\}$
Jezus
11 kwietnia 2022 at 17:20

Witam potrzebuje pomocy jak wykonac takie zadanie x-4x³-3x

Odpowiedz
Lukasz
24 stycznia 2022 at 18:13

y= pod pierwiastkiem 3 topnia sinx?????

Odpowiedz
1. Joanna Grochowska
  24 stycznia 2022 at 20:10
  
  Pierwiastek 3-go stopnia można wprowadzić wpisując potęgę (1/3).
  
  Tutaj można więc wpisać: (sinx)^(1/3)
Pola
23 października 2021 at 21:50

Witam,

jaka jest dziedzina równania

(x-4)/(x+2)=0

x+2 jest pod jednym pierwiastkiem ale nie wiem jak to napisać

Odpowiedz
1. Krystian Karczyński
  14 kwietnia 2022 at 15:02
  
  Chodzi o równanie $\frac{{x – 4}}{{\sqrt {x + 2} }} = 0$ ?
  
  Wiemy, że nie można dzielić przez zero i nie ma pierwiastka z liczby ujemnej, czyli że:
  
  $\sqrt {x + 2} \ne 0$
  
  $x + 2 \ge 0$
  
  Przekształcając oba warunki mam:
  
  $x \ne – 2$
  
  $x \ge – 2$
  
  Czyli, łącząc te dwa warunki w część wspólną
  
  $x > - 2$
  
  Zatem dziedziną tego równania jest przedział $\left( { – 2,\infty } \right)$ .
teit
25 października 2020 at 20:01

2x-1/25-x^2+\sqrt-1-x-ln(x^2-3x-10) kakulator ma chyba z tym problem

Odpowiedz
1. Krystian Karczyński
  14 kwietnia 2022 at 15:03
  
  Ja też 🙂 Co tam jest napisane? Gdzie się kończy pierwiastek?
Krystian Karczyński
3 lutego 2020 at 13:01

Pierwiastek wpisujemy jako: sqrt(…)

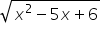
Czyli na przykład, aby wpisać w kalkulator $square root of x squared minus 5 x plus 6 end root$ , trzeba wpisać:

sqrt(x^2-5x+6)

Odpowiedz
Teofil
1 lutego 2020 at 17:46

Witam,

mam pytanie jak należy wpisać „pierwiastek” w tym kalkulatorze? Potrzebuję wyznaczyć dziedzinę funkcji f(x)=logx-1 pierwiastek z z x^2-5x+6 i nie umiem tego zapisac w kalkulatorze.

Odpowiedz
ktos
11 lutego 2017 at 15:45

Jak mam taką funkcje 1/cos(x^2) to czym jest to „n” ? w tym kalkulatorze

Odpowiedz
1. Krystian Karczyński
  14 kwietnia 2022 at 15:06
  
  Dowolną liczbą całkowitą, z zastrzeżeniami jak w wyniku tego wyznaczenia dziedziny (np. $n \ge 0$ – to dowolna liczba całkowita nieujemna).
Student
5 lutego 2015 at 16:20

Hej a mógłbyś mi wytłumaczyć dlaczego zwężam dziedzinę (odrzucam przedział od 2 do + inf) w przykładzie [((2-x)^(1/3)) / (x^2+x-6)]? Myślę, że ma to związek z liczbami zespolonymi ale nadal nie rozumiem tego.

Odpowiedz
1. Anna Zalewska
  31 października 2016 at 15:06
  
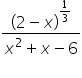
  W przykładzie $fraction numerator open parentheses 2 minus x close parentheses to the power of 1 third end exponent over denominator x squared plus x minus 6 end fraction$ pojawia się pewien problem.
  
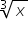
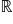
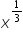
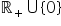
  Wiemy, że dziedziną wyrażenia $cube root of x$ jest zbiór $straight real numbers$ , ponieważ można obliczyć pierwiastek nieparzystego stopnia również z liczby ujemnej. Jednak definiuje się czasem, że dziedziną wyrażenia $x to the power of \begin inline style 1 third end style end exponent$ jest zbiór $straight real numbers subscript plus union \left curly bracket 0 \right curly bracket$ , ze względu na postać ułamkową wykładnika. Tak też liczą dziedzinę niektóre algorytmy.
  
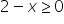
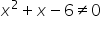
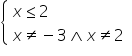
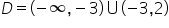
  Zapewne powyższy kalkulator wziął pod uwagę warunki: $2 minus x greater or equal than 0$ oraz $x squared plus x minus 6 not equal to 0$ . Otrzymujemy $open curly brackets table attributes columnalign \left end attributes row cell x less or equal than 2 end cell row cell x not equal to negative 3 logical and x not equal to 2 end cell end table close$ , czyli $D equals open parentheses negative infinity comma negative 3 close parentheses union open parentheses negative 3 comma 2 close parentheses$ .
  
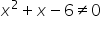
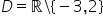
  Gdybyśmy brali pod uwagę faktyczne własności pierwiastka nieparzystego stopnia, ograniczymy się do warunku $x squared plus x minus 6 not equal to 0$ i otrzymamy dziedzinę $D equals straight real numbers \backslash \left curly bracket negative 3 comma 2 \right curly bracket$ .
  
  Trzeba przyznać, że jest to zagadnienie wyjątkowo nieprecyzyjne, jak na matematykę 😉