Currently Empty: zł0.00

Ogłoszenie
Niestety, po ponad 13 latach od udostępnienia przeze mnie darmowego kalkulatora do całek potrójnych, musiałem go “wyłączyć”.
Kalkulator był prostym “widgetem” strony WolframAlpha. Jakiś czas temu Wolframalpha zmienił swoją politykę odnośnie widgetów. Między innymi: przestały one obliczać “na miejscu”, tylko przerzucają użytkownika na stronę WolframAlpha .
Przepraszam za kłopot wszystkich dotychczasowych użytkowników Kalkulatora Do Całek Potrójnych.
Nowy kalkulator całek potrójnych
Zapraszam też do nowego kalkulatora całek potrójnych, stworzonego już przeze mnie w technologii Open Source. Dostęp do niego oraz do innych interaktywnych narzędzi możecie uzyskać w ramach subskrypcji za jedyne 5,99 zł / miesiąc (lub taniej w opcjach kilkumiesięcznych) na stronie:
A sam kalkulator wygląda tak:
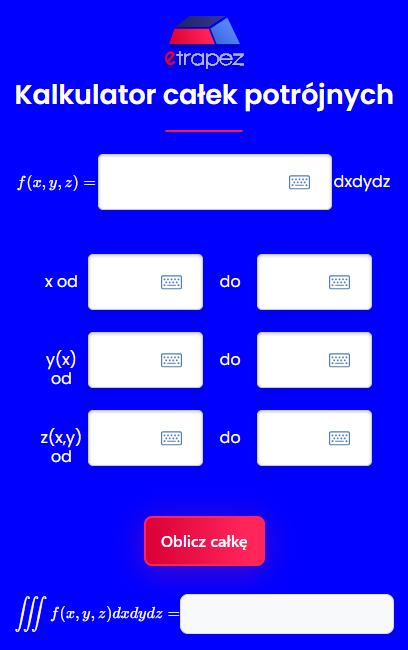
Pozdrawiam i powodzenia!
Krystian Karczyński

Asia
Jak wpisać całkę potrójną w kalkulator?
Nie rozumiem, więc poproszę o przykład.
Krystian Karczyński
Dodałem mój przykład do posta. Może jeśli masz jakieś swoje to zapodaj – pokażę, jak je wpisać w kalkulator.
Faun
Czy przed końcem maja ukaże się jeszcze kurs o całkach wielokrotnych?
Krystian Karczyński
Tak, dam radę go skończyć do końca maja.
Monika
Jej dziękuje!:D
Krystian Karczyński
A jaki Kurs Pani zamawia?
Sebastian
dziękuje 😉
ja bym chętnie pozyskał kurs całki oznaczonej 😉
PS: Dzięki poprzednim kursom zaliczyłem wszystkie kolokwia i egzamin 😉 Przede mną kolejny i czuje się na siłach aby zaliczyć na solidną ocenę.
Także jest za co dziękować.
Pozdrawiam serdecznie
Krystian Karczyński
Ogłaszam zakończenie konkursu. Wygrał p. Sebastian i p. Monika, która też podała w sumie dobrą odpowiedź, tylko nie napisała o jaką konkretnie kulę chodzi.
Sebastian
objętość kuli o promieniu 2
Sebastian
objętość obszaru kuli o promieniu 2
Krystian Karczyński
Można po prostu: objętość kuli o promieniu 2. Gratuluję 🙂
Sebastian
objętość obszaru V tej kuli 😉
Sebastian
połowa kuli? ćwierć kuli?
Krystian Karczyński
Nie. Nie.
Sebastian
wnętrza kuli,
Krystian Karczyński
Jakiego konkretnie wnętrza?
Monika
Objętość kuli!;p
Krystian Karczyński
A konkretniej czego? 🙂
Monika
Czy to nie przypadkiem pole kuli?:)
Krystian Karczyński
Nie 🙂
Sebastian
Wynik jest objętością. (V)
Krystian Karczyński
O.K. A konkretnie czego objętością?