تبديلات أويلر – لمن هذا مهم؟
تبديلات أويلر في التكاملات غير المحددة هي الخطوة التالية بعد التكاملات النسبية، التكاملات المثلثية و التكاملات مع الجذور (أو حسب بعض التصنيفات: “التكاملات غير النسبية”). هذا يعني أن معظم الطلاب لن يكون لديهم الفرصة للتعامل معها، ولم أشملها أيضاً في دورتي التدريبية على التكاملات غير المحددة.
لكن، لا يزال هناك عدد لا بأس به من الطلاب في التخصصات الرياضية، أو في التخصصات التي تتطلب معرفة رياضية قوية جداً، الذين يحتاجون لمواجهة تبديلات أويلر. وأدعو هؤلاء الطلاب (وكذلك المهتمين) للانضمام. سأناقش كل ثلاثة أنواع من تبديلات أويلر (في هذا المنشور سأتناول النوع الأول) وسأقدم مثالاً واحداً لكل منها.
هيا بنا.
أي التكاملات نحل بتبديلات أويلر؟
باستخدام تبديلات أويلر نحل التكاملات من النوع:

… أي علاقات عشوائية ![]() و
و ![]() . يمكن اعتبارها بمثابة “امتداد” لموضوع التكاملات مع الجذور (“غير النسبية”).
. يمكن اعتبارها بمثابة “امتداد” لموضوع التكاملات مع الجذور (“غير النسبية”).
نستخدم تبديلات أويلر لحل التكاملات التي لا يمكن حلها بطريقة أبسط، بالطبع. على سبيل المثال، التكامل:
![]() هو تكامل يحتوي على علاقة
هو تكامل يحتوي على علاقة ![]() و
و ![]() , لكن يمكن حله بسهولة بتبديل بسيط:
, لكن يمكن حله بسهولة بتبديل بسيط: ![]() . لذلك لا نستخدم المدفع لقتل العصفور وفي مثل هذه التكاملات البسيطة لا نعقد الأمور باستخدام أويلر.
. لذلك لا نستخدم المدفع لقتل العصفور وفي مثل هذه التكاملات البسيطة لا نعقد الأمور باستخدام أويلر.
لكن دعونا ننظر إلى التكامل:
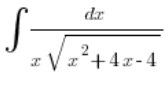
نرى أن الوضع أكثر جدية، التبديلات المعروفة سابقاً مثل ![]() أو
أو ![]() (لا يمكننا تحديد
(لا يمكننا تحديد ![]() منها) لن تحل لنا المشكلة.
منها) لن تحل لنا المشكلة.
نحتاج إلى سلاح جديد.
تبديلات أويلر – النوع الأول
عندما نواجه التكامل:

حيث ![]() ،
،
نستخدم التبديل:
![]()
، نرفع كلا الطرفين للمربع، الحدود ![]() تلغي بعضها البعض (وهذا ما نريده)، نحدد (بالترتيب):
تلغي بعضها البعض (وهذا ما نريده)، نحدد (بالترتيب):
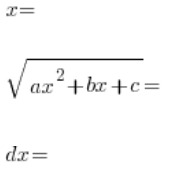
، والتي يتم التعبير عنها بعلاقات t، نقوم بتبديلها في التكامل الأصلي:

ونحصل على تكامل بمتغير t (إذا بقيت لدينا أي x-س فيه، فقد ارتكبنا خطأ) وهو تكامل نسبي.
ملاحظة
يجدر بالذكر أن العديد من الطلاب يتعلمون فقط تبديلات أويلر من النوع الأول وفقط للتكاملات من النوع:

، أي تلك التي ![]()
دعونا نتابع تبديلات أويلر من النوع الأول في العمل، على سبيل المثال:
مثال 1
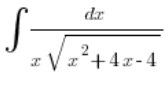
نجد أنه تكامل يحتوي على علاقة ![]() و
و ![]() . لا يمكن حله ببساطة. وأن
. لا يمكن حله ببساطة. وأن ![]() (
(![]() هو بالطبع معامل
هو بالطبع معامل ![]() , في مثالنا يساوي 1).
, في مثالنا يساوي 1).
وبالتالي سنستخدم تبديل أويلر من النوع الأول.
أقوم بالتبديل:
![]()
أي ببساطة:
![]()
أرفع كلا الطرفين إلى القوة الثانية:
![]()
الحدود التي تحتوي على ![]() تلغى من كلا الجانبين (وهذا ما يجب أن يحدث دائماً):
تلغى من كلا الجانبين (وهذا ما يجب أن يحدث دائماً):
![]()
والآن يجب تحديد ![]() ,
, ![]() و
و ![]() (بهذا الترتيب).
(بهذا الترتيب).
نبدأ بـ ![]() :
:
![]()
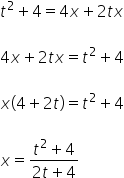
لدينا ![]() معبر عنه بمتغير t. الآن جاء دور
معبر عنه بمتغير t. الآن جاء دور ![]() , أي في مثالنا:
, أي في مثالنا: ![]() .
.
نعود إلى تبديلنا الأول، حيث كان:
![]()
الآن بما أننا نعرف ![]() (ترون لماذا الأمر مهم في الترتيب، أليس كذلك؟)، يمكننا إذًا كتابة:
(ترون لماذا الأمر مهم في الترتيب، أليس كذلك؟)، يمكننا إذًا كتابة:
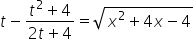
أي:
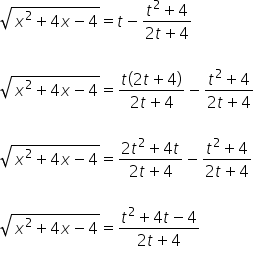
لذا لدينا ![]() معبر عنه بمتغير
معبر عنه بمتغير ![]() .
.
وأخيرًا ![]() ، والتي نحصل عليها ببساطة عن طريق التفاضل لكلا الجانبين من
، والتي نحصل عليها ببساطة عن طريق التفاضل لكلا الجانبين من ![]() المحدد:
المحدد:
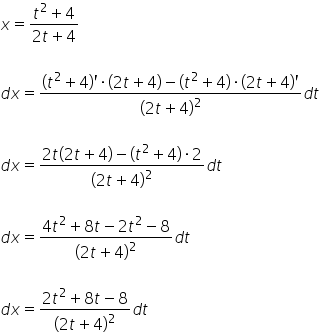
وبهذه الطريقة نحدد ![]() . لدينا إذًا:
. لدينا إذًا:
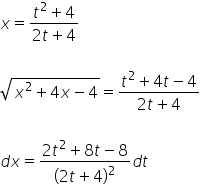
نضع كل ذلك في التكامل الأصلي:
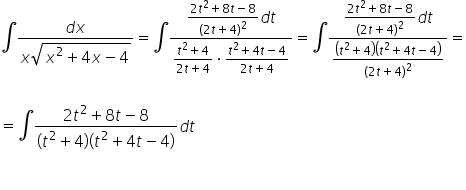
يبدو هذا في الوهلة الأولى كتكامل نسبي ممل ومعقد، لكن معروف ومخطط له (تقسيم إلى كسور جزئية، العامل الثاني في المقام يمكن تقسيمه أكثر). عادةً ما يكون الأمر كذلك، ولكن في هذا المثال الخاص سنحظى ببعض الحظ ونتجنب المرور عبر 3 صفحات من الحسابات:
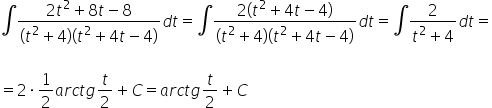
كيف نعود بالتبديل؟ في البداية كان لدينا:
![]()
من هنا بالطبع:
![]()
إذاً، النتيجة لدينا هي:
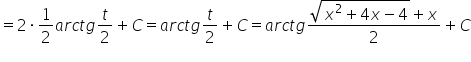
يتبع. (لدينا بعد نوعان آخران من تبديلات أويلر، ماذا لو كان معامل ![]() ليس أكبر من الصفر؟).
ليس أكبر من الصفر؟).


