قوانين الاشتقاق
الموضوع: نظرية الاشتقاق للدوال العكسية. تطبيق النظرية لاستنتاج عدة قوانين للاشتقاق.
ملخص
في محاضرتنا هذه، سنغوص في نظرية مثيرة حول اشتقاق الدوال العكسية. سنقوم بإثباتها ونرى كيف يمكن استخدامها لاستنباط مجموعة من قوانين الاشتقاق. بدون هذه النظرية، كان سيكون استنباط هذه القوانين (كما فعلنا مباشرةً من التعريفات في المحاضرة السابقة)، لنقل – معضلة صعبة.
قبل الشروع في النظرية، سيكون من الرائع معرفة ما هي الدالة العكسية، لماذا الدالة العكسية لـ ![]() هي
هي ![]() ولماذا يجب علينا أن نحد من أنفسنا في هذه الحالة إلى مجال الوسيطات مثل
ولماذا يجب علينا أن نحد من أنفسنا في هذه الحالة إلى مجال الوسيطات مثل ![]() …
…
استخدام النظرية لاستنباط القوانين هو مهمة شائعة جدًا في حساب التفاضل والتكامل على مستوى الجامعة، لذا قد تنقذ هذه المحاضرة حياتك الأكاديمية يومًا ما.
أنا أقتبس النظرية والبرهان من كتاب فختنهولتز، مع تعديلها هنا وهناك، تصحيح الأخطاء الطباعية، وإجراء بعض التغييرات.
نظرية الاشتقاق للدوال العكسية
إذا كانت الدالة ![]() لها دالة عكسية
لها دالة عكسية ![]() , وفي النقطة
, وفي النقطة ![]() لها مشتقة محددة وغير صفرية
لها مشتقة محددة وغير صفرية ![]() , عندئذٍ في النقطة المقابلة
, عندئذٍ في النقطة المقابلة ![]() توجد مشتقة للدالة العكسية
توجد مشتقة للدالة العكسية 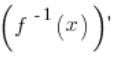 وقيمتها في النقطة
وقيمتها في النقطة ![]() تساوي
تساوي 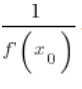 .
.
هل تشعر بالحيرة من هذا التتابع من الرموز؟ في البداية، من المحتمل جدًا، ولكن دعونا نتعمق في هذه النظرية من خلال بعض الأمثلة البسيطة والمحددة.
بالطبع، إليك ترجمة نفس المقطع إلى اللغة العربية مع الحفاظ على نبرة غير رسمية ومرحة مع استخدام مصطلحات رياضية متخصصة: —مثال 1
إذا كانت الدالة
لديها دالة معكوسة
,
1. لنأخذ الدالة ![]() في الفترة
في الفترة ![]()
2. الدالة المعكوسة لها موجودة وهي ![]() – لن أشرح لماذا وسبب هذا القيد على فترة x، عذراً…
– لن أشرح لماذا وسبب هذا القيد على فترة x، عذراً…
وفي النقطة
لديها مشتقة محدودة وغير صفرية
,
3. لنأخذ النقطة ![]() . مشتقة الدالة
. مشتقة الدالة ![]() موجودة (
موجودة (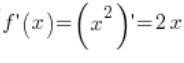 ) وفي النقطة
) وفي النقطة ![]() قيمتها غير صفرية (
قيمتها غير صفرية (![]() ).
).
ثم في النقطة المقابلة لـ
النقطة
4. النقطة المقابلة لـ ![]() هي قيمة الدالة
هي قيمة الدالة ![]() في النقطة
في النقطة ![]() , أي
, أي 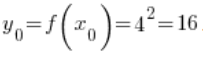 .
.
في مثالنا:
![]()
مشتقة الدالة المعكوسة
موجودة
5. بالفعل، الدالة المعكوسة هي ![]() ، ومشتقتها تساوي:
، ومشتقتها تساوي: 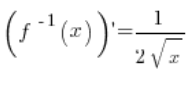 (من الصيغ الأساسية للمشتقات) وفي النقطة
(من الصيغ الأساسية للمشتقات) وفي النقطة ![]() موجودة بالتأكيد وتساوي:
موجودة بالتأكيد وتساوي:
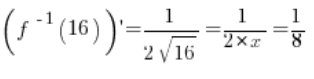
وقيمتها في النقطة
تساوي
.
6. بالفعل، القيمة المحسوبة في النقطة 5. 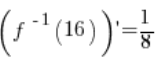 تساوي:
تساوي:
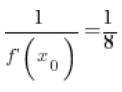 (
(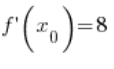 – حسبت هذا في النقطة 3.)
– حسبت هذا في النقطة 3.)
أي أن النظرية “تعمل” 🙂
مثال 2
إذا كانت الدالة
لديها دالة معكوسة
,
1. لنأخذ الدالة الأُسية ![]()
2. الدالة المعكوسة لها موجودة وهي ![]() – هذا كان في المتوسطة، لن أشرح مرة أخرى (الدوال اللوغاريتمية والأُسية هي دوال معكوسة لبعضها)
– هذا كان في المتوسطة، لن أشرح مرة أخرى (الدوال اللوغاريتمية والأُسية هي دوال معكوسة لبعضها)
وفي النقطة
لديها مشتقة محددة ومختلفة عن الصفر
,
3. لنأخذ النقطة ![]() . مشتقة الدالة
. مشتقة الدالة ![]() موجودة (
موجودة (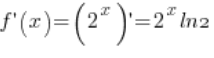 – الصيغ الأساسية للمشتقات) وفي النقطة
– الصيغ الأساسية للمشتقات) وفي النقطة ![]() قيمتها مختلفة عن الصفر (
قيمتها مختلفة عن الصفر (![]() ).
).
ثم في النقطة المقابلة لـ
النقطة
4. النقطة المقابلة لـ ![]() هي قيمة الدالة
هي قيمة الدالة ![]() في النقطة
في النقطة ![]() ، أي
، أي 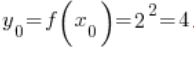 .
.
إذن:
![]()
توجد مشتقة الدالة المعكوسة
5. فعلاً، الدالة المعكوسة هي ![]() ، ومشتقتها تساوي:
، ومشتقتها تساوي: 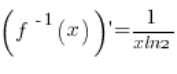 (وفقاً للصيغ الأساسية للمشتقات). في النقطة
(وفقاً للصيغ الأساسية للمشتقات). في النقطة ![]() المشتقة موجودة وتساوي:
المشتقة موجودة وتساوي:
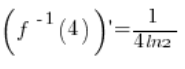
وقيمتها في النقطة
تساوي
.
6. بالفعل، القيمة المحسوبة في النقطة 5. 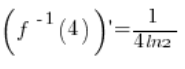 تساوي:
تساوي:
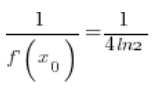 (
(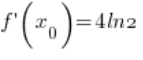 – قمت بحساب ذلك في النقطة 3.)
– قمت بحساب ذلك في النقطة 3.)
إذن، النظرية “تعمل” مرة أخرى 🙂
إثبات نظرية مشتقة الدالة العكسية
سنثبت هذه النظرية معتمدين على التفسير الهندسي لمشتقة الدالة في نقطة. كما نتذكر، قيمة مشتقة الدالة في نقطة هي جيب التمام لميل المماس لمنحنى الدالة في تلك النقطة.
في الرسم البياني يبدو الأمر كالتالي:
 قيمة المشتقة في نقطة
قيمة المشتقة في نقطة ![]() عرفناها في المحاضرات السابقة كجيب تمام الزاوية
عرفناها في المحاضرات السابقة كجيب تمام الزاوية ![]()
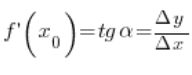
دعونا الآن نلاحظ أمراً مثيراً للاهتمام: يمكن تمثيل رسم الدالة العكسية لـ ![]() على نفس الرسم البياني، ولكن يجب أن نتذكر قراءته “بشكل معكوس” – أي كأننا نعطي قيم y للمتغيرات x (وبالتالي فإن زيادة المتغيرات في الدالة العكسية هي
على نفس الرسم البياني، ولكن يجب أن نتذكر قراءته “بشكل معكوس” – أي كأننا نعطي قيم y للمتغيرات x (وبالتالي فإن زيادة المتغيرات في الدالة العكسية هي ![]() ، وزيادة القيم المقابلة لها هي
، وزيادة القيم المقابلة لها هي ![]() ):
):
 لنلاحظ أن قيمة مشت
قة هذه الدالة العكسية في نقطة
لنلاحظ أن قيمة مشت
قة هذه الدالة العكسية في نقطة ![]() تساوي:
تساوي:
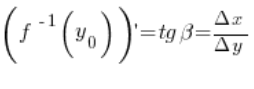
إذن، نرى أن قيم المشتقات للدالة ودالتها العكسية هي جيوب تمام الزوايا في نفس المثلث القائم.
وهذه الجيوب التمام للزوايا في مثلث قائم (كما نتذكر من المدرسة الثانوية) مرتبطة بالعلاقة:
![]()
إذًا (بعد القسمة على كلا الجانبين بـ ![]() ):
):
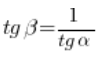
ومن هنا يترتب استنتاج نظريتنا، أي:
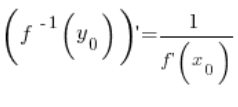
🙂
نهاية الإثبات
اشتقاق صيغ للمشتقات باستخدام نظرية المشتقة للدالة المعكوسة
مثال 3
اشتق صيغة لمشتقة الدالة ![]() .
.
الصيغة التي يجب علينا اشتقاقها هي: 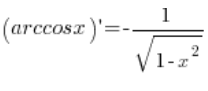 .
.
دالتنا f(x) هي دالة arccosx. الدالة المعكوسة لها هي ![]() . المشتقة من الدالة المعكوسة هي
. المشتقة من الدالة المعكوسة هي 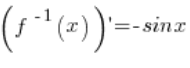 .
.
وفقاً لنظرية المشتقة للدالة المعكوسة، فإن قيمة المشتقة للدالة المعكوسة في النقطة ![]() تساوي مقلوب قيمة المشتقة للدالة في النقطة
تساوي مقلوب قيمة المشتقة للدالة في النقطة ![]() :
:
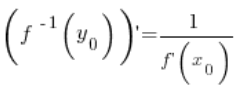
أي في أي نقطة ![]() :
:
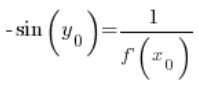
بعد التحويل:
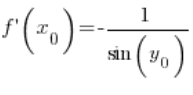
باستخدام الهوية التريغونومترية، يمكننا استنتاج أن: 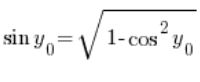 , وبالتالي لدينا:
, وبالتالي لدينا:
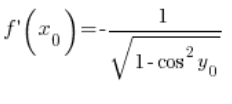
الآن انتبه: ![]() هو قيمة الدالة
هو قيمة الدالة ![]() في النقطة
في النقطة ![]() ، وهو
، وهو 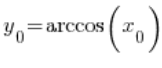 . وبالتالي:
. وبالتالي:
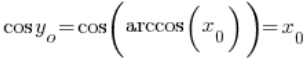 – لأن جيب التمام والجيب التمام المعكوس هما دالتان معكوستان، لدينا إذًا:
– لأن جيب التمام والجيب التمام المعكوس هما دالتان معكوستان، لدينا إذًا:
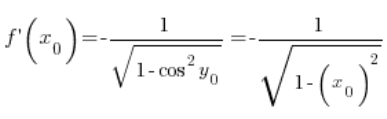 في أي نقطة
في أي نقطة ![]() (مع مراعاة الشروط المتعلقة بالمجال، التي تجاهلتها)، وبالتالي تم إثبات صيغتنا
(مع مراعاة الشروط المتعلقة بالمجال، التي تجاهلتها)، وبالتالي تم إثبات صيغتنا 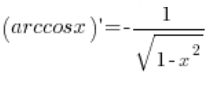 بهذه الطريقة.
بهذه الطريقة.
مثال 4
اشتق صيغة لمشتقة الدالة ![]() .
.
الصيغة التي يجب علينا اشتقاقها هي: 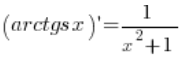 .
.
دالتنا f(x) هي دالة arctgx. الدالة المعكوسة لها هي ![]() . المشتقة من الدالة المعكوسة هي
. المشتقة من الدالة المعكوسة هي 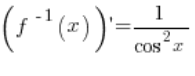 .
.
وفقًا لنظرية المشتقة للدالة المعكوسة، فإن قيمة المشتقة للدالة المعكوسة في النقطة ![]() تساوي مقلوب قيمة المشتقة للدالة في النقطة
تساوي مقلوب قيمة المشتقة للدالة في النقطة ![]() :
:
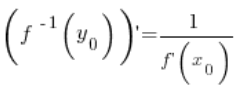
أي في أي نقطة ![]() :
:
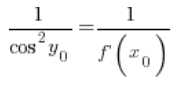
بعد التحويل:
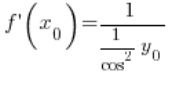
باستخدام الهوية التريغونومترية، يمكننا تحويلها أكثر:
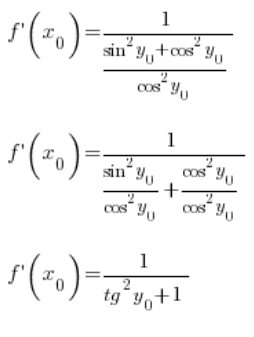
الآن انتبه: ![]() هو قيمة الدالة
هو قيمة الدالة ![]() في النقطة
في النقطة 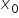 ، وهو
، وهو 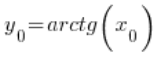 . وبالتالي:
. وبالتالي: 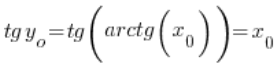 – لأن الظل والظل المعكوس هما دالتان معكوستان، لدينا إذًا:
– لأن الظل والظل المعكوس هما دالتان معكوستان، لدينا إذًا:
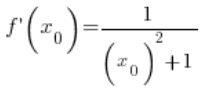 في أي نقطة
في أي نقطة ![]() (مع مراعاة الشروط المتعلقة بالمجال، التي تجاهلتها)، وبالتالي تم إثبات صيغتنا
(مع مراعاة الشروط المتعلقة بالمجال، التي تجاهلتها)، وبالتالي تم إثبات صيغتنا 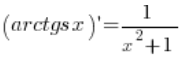 بهذه الطريقة.
بهذه الطريقة.
نهاية
عند كتابة هذا المقال، استخدمت…
1. “التفاضل والتكامل. الجزء الأول.” لـ G.M. Fichtenholz. النشر في عام 1966.
اضغط هنا لتذكر كيفية اشتقاق صيغ المشتقات من التعريف (المحاضرة السابقة) <–
اضغط هنا لرؤية كيف يمكن إثبات خصائص المشتقات (المحاضرة التالية) –>
