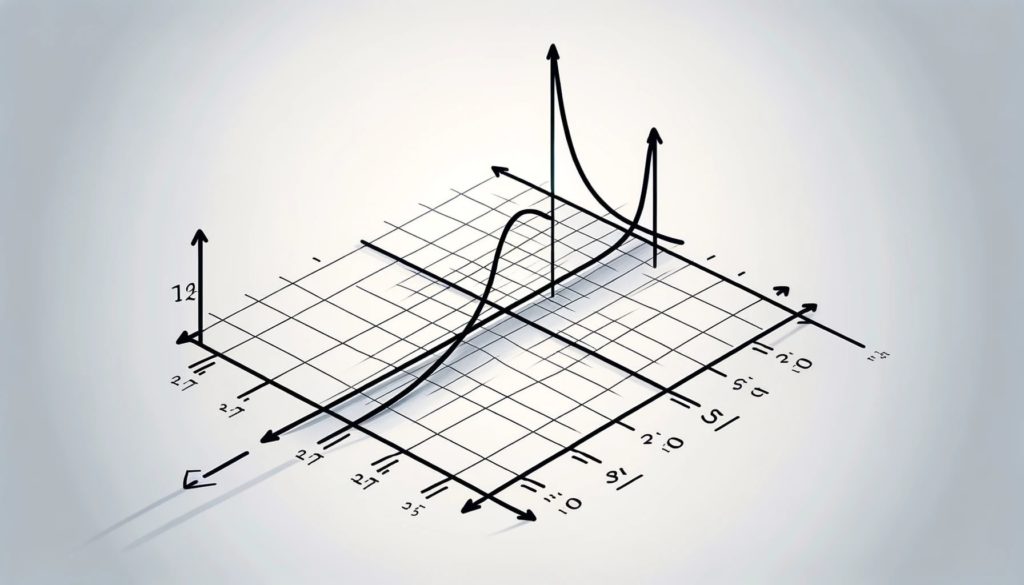
العلاقة بين الأسيمبتوتات الأفقية والمائلة هي كالتالي: الأسيمبتوتات الأفقية هي حالات خاصة من الأسيمبتوتات المائلة. بمعنى أن كل أسيمبتوت أفقي هو أيضاً أسيمبتوت مائل، ولكن ليس كل مائل هو أفقي.
يمكن ويجب استخدام هذا لتسهيل عملية حساب أسيمبتوتات الدالة. هناك نهجان أساسيان لهذا الموضوع:
1. أولاً، نحسب الأسيمبتوتات الأفقية
هذا النهج موضح في دورتي التعليمية بالفيديو حول تحليل سلوك الدوال.
شرط وجود أسيمبتوت أفقي لدالة هو:
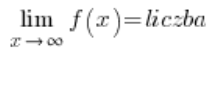 أو
أو 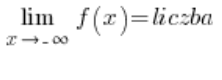
– نتذكر أن الأفقية هي نوع من المائلة). ولكن، إذا لم تظهر لنا الأسيمبتوتات الأفقية فإننا نواجه مشكلة – يتعين علينا حساب الأسيمبتوتات المائلة من جديد.
بالطبع، الوضع أكثر تعقيدًا قليلاً: قد تظهر الأسيمبتوتا الأفقية في ![]() , ولا تظهر في
, ولا تظهر في ![]() . في هذه الحالة، لن ندرس وجود الأسيمبتوت المائل في
. في هذه الحالة، لن ندرس وجود الأسيمبتوت المائل في ![]() (لأنها ظهرت هناك بالفعل)، ولكن يتعين علينا فحص وجودها في
(لأنها ظهرت هناك بالفعل)، ولكن يتعين علينا فحص وجودها في ![]() .
.
2. أولاً، نحسب الأسيمبتوتات المائلة
…وبعدها ستظهر الأسيمبتوتات الأفقية تلقائيًا (أو لا)، وسيتعين علينا فقط تفسير الإجابات بشكل صحيح. هذا النهج لا أعرضه في دورتي. العيب هو أن شروط وجود أسيمبتوت مائل للدالة أكثر تعقيدًا قليلاً:
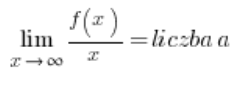 و
و 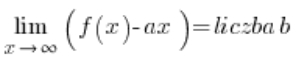
أو:
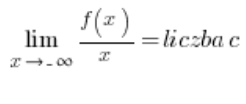 و
و 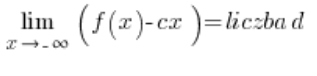
…والميزة هي أنه بمجرد حسابها، لا يتعين عليك القيام بأي حسابات إضافية. إذا تم استيفاء الشروط وكان الرقم ![]() (أو
(أو ![]() ) من شروط وجود الأسيمبتوت المائل يساوي
) من شروط وجود الأسيمبتوت المائل يساوي ![]() ، فهذا يعني أن الأسيمبتوت المائل هو في الواقع أسيمبتوت أفقي.
، فهذا يعني أن الأسيمبتوت المائل هو في الواقع أسيمبتوت أفقي.
لتقصير العمل إضافيًا، يمكننا حساب مباشرة:
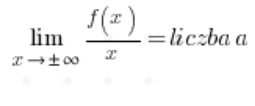 و
و 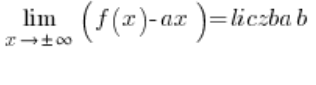
وتقسيم الحساب للشروط المنفصلة لـ ![]() و
و ![]() فقط عند الضرورة (عندما يكون هناك فرق في النتيجة، سواء كان x يتجه إلى
فقط عند الضرورة (عندما يكون هناك فرق في النتيجة، سواء كان x يتجه إلى ![]() , أو إلى
, أو إلى ![]() ).
).