Asymptoty poziome i ukośne funkcji
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Związek pomiędzy asymptotami poziomymi i ukośnymi jest następujący: asymptoty poziome są szczególnymi asymptotami ukośnymi. Każda asymptota pozioma zatem jest asymptotą ukośną, ale nie każda ukośna jest poziomą.
Można i należy to wykorzystać, aby skrócić sobie liczenie asymptot funkcji. Możliwe są bowiem dwa zasadnicze podejścia do tego tematu:
1. Najpierw liczymy asymptoty poziome
To podejście pokazuję w moim Kursie Video dotyczącym badania przebiegu zmienności funkcji.
Warunkiem na istnienie asymptoty poziomej funkcji jest:
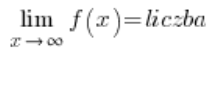lub 
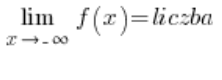
Jeżeli wyjdą nam asymptoty poziome, nie liczymy już ukośnych (bo jest tak, jakby ukośne nam już wyszły – pamiętamy, że poziome to ukośne). Jednak jeżeli poziome nam nie wyjdą to mamy kłopot – musimy od nowa liczyć asymptoty ukośne.
Oczywiście sytuacja jest trochę bardziej skomplikowana: asymptota pozioma może nam “wyjść” w 
, a “nie wyjść” w 
. W takim przypadku nie badalibyśmy istnienia asymptoty ukośnej w (bo już nam tam wyszła), ale musielibyśmy badać jej istnienie w .
2. Najpierw liczymy asymptoty ukośne
…i wtedy asymptoty poziome wyjdą nam (albo i nie) automatycznie, trzeba będzie tylko właściwie zinterpretować odpowiedzi. Tego podejścia nie pokazuję w moim Kursie. Minusem jest to, że na istnienie asymptoty ukośnej funkcji są troszeczkę bardziej skomplikowane warunki:
i 
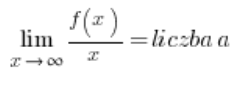
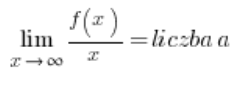
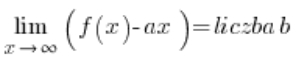
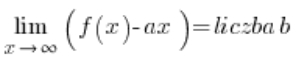
lub:
i 
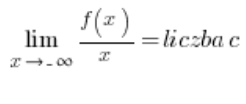
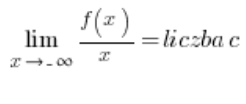
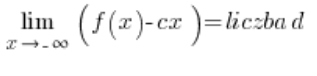
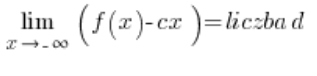
…a plusem jest to, że jak już je policzymy nie trzeba liczyć nic dalej. Jeżeli warunki są spełnione i liczba 
(lub 
) z warunków na istnienie asymptoty ukośnej wyjdzie równa 
, to znaczy, że asymptota ukośna jest asymptotą poziomą.
Żeby dodatkowo skrócić sobie robotę, można liczyć od razu:
i 
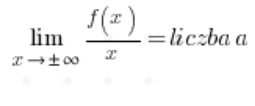
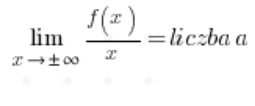
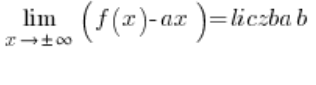
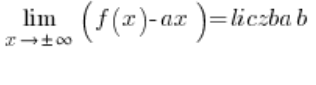
A rozbicie na liczenie osobno warunków dla 
i 
tylko wtedy, kiedy będzie to konieczne (kiedy będzie robiło różnicę w wyniku, czy x dąży do , czy do .
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
Jedne z najlepiej wydanych pieniędzy w ostatnim czasie:) . Najpierw w semestrze 1 kurs rozjaśnił mi macierze 🙂 które wydawały się kosmosem (ostatni raz w ławce szkolnej siedziałem w 1992 roku jak pisałem maturę 🙂 ), egzamin za 1 razem , a teraz ciągi i pochodne zaczynam łapać i raczej bez stresu podejdę do kolokwium 🙂 Wielkie dzięki!! Jedyna uwaga to to , że w kursie o pochodnych brakuje trochę zadań z parametrem (typu dla jakich wartości a i b funkcja ma asymptoty pionowe itp. ) . Niestety mój wykładowca ma wielkie wymagania a czasu na robienie przykładów brak , w ciągu 9 h wykładu przeszliśmy przez ciągi , granice , badanie funkcji ( monotoniczności , przegięcia itd ) oraz początek całek !! bez Trapeza pewna porażka 🙂
Dzięki!
Mam zbadac funckje 2x-sinx
Wiadomo pionowe nie istnieja , a ukośne według odpowiedzi tez nie .
Ale wychodzi mi ze lim f(x)/x=2
A b wcale nie wychodzi (lim sinx) I
I co teraz?
Witam, czy byłaby możliwość na podstawie tego: f(2)=f(5)=lim(x->+oo)f(x)=lim(x->2+)f(x)=lim(x->-2-)f(x)=2lim(x->-oo)f(x)=lim(x->-2+)f(x)=lim(x->5)f(x)=f(1)=0lim(x->2-)f(x)=lim(x->6)f(x)=+oostwierdzić, czy*f ma trzy asymptoty pionowe*f ma jedną asymptotę poziomą*f nie ma asymptoty ukośnejMogę prosić o pomoc? Z góry dziękuję 🙂
Witam, mam problem z asypmtotami funkcji ( e ^ ( x ^ 2 ) ) – 1. Mogę prosić o pomoc?
Jak policzyć asymptotę y=xe^2x
Zapraszam do filmiku:
https://www.youtube.com/watch?v=Va6JlakGmvA
Witam,Czu mogę prosić o pomoc w obliczeniu tego zadania? f(x)=
Mam wyznaczyć asymptotę ukośną funkcji f oraz zbadać monotoniczność funkcji f w przedziale 
Niestety w sobotę egzamin , a ja na tym utknęłam, bo nie rozumiem tego zupełnie
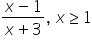
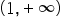
Jak należałoby obliczyć asymptoty z y=x^3/x-1?
Witam.Chciałam zapytać co wtedy, gdy z dziedziny funkcji “wypadają” nam jakieś liczby, ale granice w tych punktach istnieją?Np. dziedziną funkcji jest
, ale granica w 1 istnieje. Czy wtedy x=1 jest asymptotą poziomą?
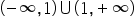
Pani Anno,
w takim przypadku prosta
nie jest asymptotą.
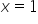
Asymptotę pionową prawo- lub lewostronną mamy, gdy granica odpowiednio prawo- lub lewostronna funkcji w punkcie, który nie należy do dziedziny, wynosi
.
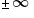
Asymptotę poziomą mamy, gdy granica funkcji w
(asymptota pozioma prawostronna) lub w 
(asymptota pozioma lewostronna) istnieje i jest równa pewnej stałej liczbie.
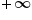
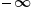
Jak wyznaczyć asymptotę dla y=xe^1/2 oraz y=xe do potęgi 1/x
Funkcja
jest funkcją liniową. Może lepiej to będzie widać, jak zapiszemy ją w ten sposób: 
. Funkcja liniowa nie ma żadnych asymptot, niezależnie od jej współczynników.
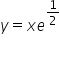
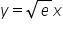
Sposób wyznaczenia asymptot funkcji
znajdziemy w filmiku:
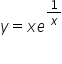
https://www.youtube.com/watch?v=y_B1G5TmdUw&feature=share
a jak wyznaczać asymptoty takiej funkcji: y=x arcctg 1/xBardzo proszę o odpowiedź i z góry dziękuję! 🙂
Aby wyznaczyć asymptoty funkcji
postępujemy zgodnie ze schematem podanym powyżej.
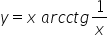
1. Asymptoty pionowe
To oznacza, że nie ma asymptoty pionowej. Dodatkowo poniżej wykres funkcji
2. Asymptoty poziome
Stąd wniosek, że nie ma asymptot poziomych.
3. Asymptoty ukośne
Stąd
.
Dalej
Stąd
.
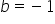
Tym samym asymptotą ukośną obustronną jest prosta
.
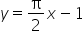
A jak się zabrać za coś takiego:
?Należy wyznaczyć wykres asymptoty ukośnej.
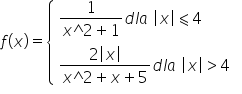
Korzystając ze wzorów na a i b wyliczamy współczynniki dla prostej
będącej asymptotą ukośną. Będziemy korzystać ze wzoru 2 funkcji ponieważ granice będą w 
.
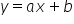
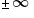
Mamy kolejno
-> dla asymptoty prawostronnej
czyli
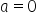
czyli
. Stąd asymptota ukośna prawostronna (a właściwie pozioma) ma równanie 
.
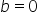
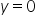
-> dla asymptoty lewostronnej
czyli
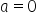
czyli
. Stąd asymptota ukośna lewostronna (a właściwie pozioma) ma równanie 
.
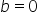
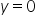
a jak a=b ? to są te ukośne czy nie?
Tak, oczywiście są ukośne 😉
Np. a=b=2 będziemy mieli asymptotę postaci y=2x+2.
W przypadku gdy a=b=0 to będziemy mieli asymptotę postaci y=0, czyli asymptotę poziomą (a taka też jest ukośną) 🙂
A jak obliczyć asymptoty ukośne w tej funkcji: y=lnx/x. ??
Rozwiążę ten przykład od początku:
\displaystyle y=\frac{{ln x}}{x}
1. Dziedzina
— x>0 (ze względu na logarytm)
— \displaystyle x\ne 0 (z mianownika ułamka)
czyli:
\displaystyle Dy:x\in (0,\infty )
2. Asymptoty pionowe.
\displaystyle \underset{{x\to {{0}^{+}}}}{\mathop{{lim }}}\frac{{ln x}}{x}=\left[ {\frac{{-\infty }}{{{{0}^{+}}}}} \right]=-\infty
\displaystyle \underset{{x\to {{0}^{-}}}}{\mathop{{lim }}}\frac{{ln x}}{x}=\left[ {\frac{{-\infty }}{{{{0}^{-}}}}} \right]=\infty
Mam więc asymptotę pionową \displaystyle x=0Prawostronną (biorę tylko jednostronną ze względu na dziedzinę).
UWAGA.
W podstawieniu granicy wyszło mi nieskończoność przez zero. Jednak NIE jest to symbol nieoznaczony. Nieskończoność przez zero to symbol wyrażenia, w którym licznik przyjmuje wartości nieskończenie wielkie, a mianownik nieskończenie małe (w sensie nieskończenie bliskie zera (nie \displaystyle {-\infty })
Można to porównać ze wzorem na granicę \displaystyle \left[ {\frac{A}{0}} \right], gdzie ta stała A jest bardzo bardzo duża po prostu.
3. Asymptoty ukośne/poziome.
\displaystyle \underset{{x\to \infty }}{\mathop{{lim }}}\frac{{\frac{{ln x}}{x}}}{x}=\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{ln x}}{{{{x}^{2}}}}\underset{H}{\overset{{\left[ {\frac{\infty }{\infty }} \right]}}{\mathop{=}}}\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{\left( {ln x} \right)’}}{{\left( {{{x}^{2}}} \right)’}}=\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{\frac{1}{x}}}{{2x}}=\underset{{x\to \infty }}{\mathop{{lim }}}\frac{1}{{2{{x}^{2}}}}=\left[ {\frac{1}{\infty }} \right]=0
\displaystyle \underset{{x\to \infty }}{\mathop{{lim }}}\left( {\frac{{ln x}}{x}-0\cdot x} \right)=\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{ln x}}{x}\underset{H}{\overset{{\left[ {\frac{\infty }{\infty }} \right]}}{\mathop{=}}}\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{\left( {ln x} \right)’}}{{\left( x \right)’}}=\underset{{x\to \infty }}{\mathop{{lim }}}\frac{{\frac{1}{x}}}{1}=\underset{{x\to \infty }}{\mathop{{lim }}}\frac{1}{x}=0
Mam więc asymptotę poziomą \displaystyle y=0.
czy w tym przykładzie nie powinno sie zbadac tez lim x→(-∞) dla asymptot ukośnych mimo że dziedzina to x>0? robię podobny przykład tylko z pierwiastkiem w mianowniku i nie zgadza mi sie również ze y=0 mogloby byc asymptota poziomą bo wykres przecina OX w x=1 wiec to sie wzajemnie wyklucza. Prosze o pomoc !!
Jak obliczyć asymptoty ukośne tutaj : x^2+1/x
Pozwoliłem sobie zinterpretować wzór funkcji tak: f\left( x \right)=\frac{{{x}^{2}}+1}{x}(inaczej wykres nie miałby w ogóle asymptot ukośnych)
Liczę przy x->oo :
\underset{x\to \infty }{\mathop{lim }}\frac{\tfrac{{{x}^{2}}+1}{x}}{x}=\underset{x\to \infty }{\mathop{lim }}\frac{{{x}^{2}}+1}{x}\cdot \frac{1}{x}=\underset{x\to \infty }{\mathop{lim }}\frac{{{x}^{2}}+1}{{{x}^{2}}}=\underset{x\to \infty }{\mathop{lim }}\frac{{{x}^{2}}\left( 1+\tfrac{1}{{{x}^{2}}} \right)}{{{x}^{2}}}=1
\underset{x\to \infty }{\mathop{lim }}\left( \frac{{{x}^{2}}+1}{x}-1\cdot x \right)=\underset{x\to \infty }{\mathop{lim }}\left( \frac{{{x}^{2}}+1}{x}-\frac{{{x}^{2}}}{x} \right)=\underset{x\to \infty }{\mathop{lim }}\left( \frac{1}{x} \right)=0
i przy x -> -oo :
\underset{x\to -\infty }{\mathop{lim }}\frac{\tfrac{{{x}^{2}}+1}{x}}{x}=1– korzystając z poprzednich obliczeń
\underset{x\to \infty }{\mathop{lim }}\left( \frac{{{x}^{2}}+1}{x}-1\cdot x \right)=0– korzystając z poprzednich obliczeń
Piszę odpowiedź: y=x jest asymptotą ukośną badanej funkcji zarówno przy x->oo, jak i x-> -oo.
Co potwierdza wykres funkcji f\left( x \right)=\frac{{{x}^{2}}+1}{x}:
mam problem z wyznaczeniem asympmtot w takim przykładzie 3stopnia√x^2−x
Chodzi o coś takiego:
y=\sqrt[ 3]{{{x}^{2}}-x}?
“- x” jest za pierwiastkiem
Badam następującą funkcję: y=((x^3)-1)/((x^2)-4). Policzyłam asymptoty pionowe i wyszły mi x=-2 oraz x=2 (i jest to zgodne z wykresem). Policzyłam również asymptotę ukośną i wyszła mi y=x, ale nie jestem pewna czy jest to poprawne (podejrzewam, że popełniłam błąd). Proszę o pomoc
W przypadku asymptot ukośnych (od razu obustronne można liczyć bo wyniki będą podobne) obliczenia powinny być następujące:
czyli
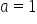
czyli
. Stąd asymptota ukośna obustronna ma równanie 
.
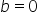
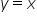
a mój wykładowca liczy asymptote poziomą normalnie na żywca tzn żę lim dąży do nieskaczonosci z wzoru na funkcje tego co na poczatku zadania…mozna tak?
co jeżeli przy liczeniu granicy funkcji przy x -> +nieskończoności wychodzi nieskończoność, a przy x-> -nieskończoności wychodzi liczba 0.
sprawdzam wtedy ukośne tylko przy x_. do -nieskoncznosci czy do +nieskonczonosci rowniez?
ok, już wiem, że wtedy badam ukośną tylko przy x-> +nieskończoności 🙂
Witam!
Mam taki problem. takie zadanie y= 1/x^2
Df x różny od 0
więc liczymy granice w -0 i +0 i obie wychodzą +nieskończoność
więc asymptota pionowa jest prawo Stronna, a w odpowiedziach jest obustronna dlaczego??
Witam!
Granica w -0 wyszła nam nieskończoność (nieważne, czy +nieskończoność, czy -nieskończoność) -> zatem jest asymptota pionowa lewostronna.
Granica w +0 wyszła nam nieskończoność (nieważne, czy +, czy -) -> zatem jest asymptota pionowa prawostronna.
Istnieje granica lewostronna i istnieje granica prawostronna -> zatem istnieje granica obustronna.
Widać to dobrze na wykresie funkcji:
Witam, mam pytanie odnośnie funkcji y=(x^2 + 4) / x. jakie ona ma asymptoty i ukośne i poziome ? może ktoś wyjaśnić ?
mam problem jak wyznaczyc asymptotę z takiej funkcji f(x)=x-arc tgx
Wyznaczyłem tutaj, zapraszam:
Dlaczego nie można tego przykładu policzyć za pomocą reguły De L’Hospitala? Przy x->nieskończoność:
(x-arctgx)/x daje nam symbol [nieskończoność/nieskończoność].
Licząc pochodne wychodzi:
[1+1/(x^2+1)]/1, czyli (x^2+2)/(x^2+1).
Wyciągamy x^2 przed nawias, skracamy i wychodzi 1.
Pozdrawiam!
(x-arctgx)/x daje symbol [nieskończoność – nieskończoność/nieskończoność], ponieważ x-arctgx przy x–>nieskończoności daje wyrażenie nieoznaczone [nieskończoność-nieskończoność], a nie tak jak napisałeś [nieskończoność]. Ponieważ dzieje się tak, musimy zrobić to w taki sposób, w jaki zrobił to Pan Karczyński.
Pozdrawiam 🙂
Dla potomnych: Zarówno Pan Karczyński, jak i użytkownik Bartosz Student AiR piszą bzdury. Oczywiście jest to symbol nieoznaczony [nieskończoność/nieskończoność] i jak najbardziej ów granicę można policzyć stosując regułę de L’Hospitala (czy jest to sposób optymalny to oczywiście inny temat).Pozdrawiam.
a jeżeli mam funkcję x^3-x^2-2x / x^2+x-6 to co wtedy? bo nie jestem pewna..
ten pierwszy już wiem 🙂 ale problem mam z takim przykładem x^3+2x^2-x-1 / x^2+3x+2 , nie mam pojęcia jak to rozpisać, dzieliłam wielomiany przez siebie ale to też nic mi nie dało, nie wiem co i jak.
Witam. Mam pytanie czy jest możliwość żeby funkcji nie miała w ogóle asymptot ? Żadnych.. ?
Oczywiście, tak. Np. funkcja f(x)=sin x
Dokładnie. Pełno funkcji nie ma asymptot.
A co jeżeli mam policzyć asymptoty dla funkcji
f(x) = pierw. z x^2+1
——————-
x
Czy to możliwe, żeby asymptoty poziome wyszły +nieskończoność i – nieskończoność i po policzeniu skośnych dla +nieskończoności wyszło 1? Wydaje mi się, że nie umiem za bardzo wykonywać działań z pierwiastkami 🙂
A jest jakas zasada np gdy w dziedzinie wychodzi nam przedzial (-1,1] i bedzie asymptota pionowa w x=-1 to mozna od razu stwierdzic ze nie bedzie ukosnych?
Mialem wlasnie problem z obliczeniem ukosnych, wrzucilem zadania na forum i dostalem od razu odpowiedz ze skoro jest tylko taki jeden przedzial, to nie bedzie ukosnych.
(Funckcja jest taka: f(x) = \sqrt{ {1-x} / {1+x} } )
No tak, w pewnym sensie “jest taka zasada” asymptoty ukośne mogą istnieć tylko dla x\to \infty lub x\to -\infty tak więc gdy dziedziną funkcji jest przedział x\in \left( -1,1 \right) , to nie ma nawet gdzie jej szukać i oczywiście nie istnieje.
Ale nie jest to kwestia jakiś asymptot pionowych.
kurcze, jakbys tak jeszce zadnie jakies dal 😀
No weźmy na przykład funkcję \left( x \right)=\frac{1+x}{1-x}
Licząc pierwszym podejściem liczę najpierw asymptoty poziome:
\underset{x\to \infty }{\mathop{lim }}\frac{1+x}{1-x}=\underset{x\to \infty }{\mathop{lim }}\frac{x\left( \frac{1}{x}+1 \right)}{x\left( \frac{1}{x}-1 \right)}=-1
\underset{x\to -\infty }{\mathop{lim }}\frac{1+x}{1-x}=\underset{x\to -\infty }{\mathop{lim }}\frac{x\left( \frac{1}{x}+1 \right)}{x\left( \frac{1}{x}-1 \right)}=-1
Stwierdzam więc, że asymptoty poziome istnieją (przy x\to \infty i x\to -\infty , o równaniu y=-1) i ukośnych już nie szukam. Bo poziome to są właśnie szczególne ukośne.
Licząc drugim podejściem liczę najpierw asymptoty ukośne:
\underset{x\to \infty }{\mathop{lim }}\frac{\frac{1+x}{1-x}}{x}=\underset{x\to infty }{\mathop{lim }}\frac{1+x}{x-{{x}^{2}}}=\underset{x\to \infty }{\mathop{lim }}\frac{x\left( \tfrac{1}{x}+1 \right)}{{{x}^{2}}\left( \tfrac{1}{x}-1 \right)}=0
\underset{x\to \infty }{\mathop{lim }}\left( \frac{1+x}{1-x}-0\cdot x \right)=-1
\underset{x\to -\infty }{\mathop{lim }}\frac{\frac{1+x}{1-x}}{x}=\underset{x\to -\infty }{\mathop{lim }}\frac{1+x}{x-{{x}^{2}}}=\underset{x\to -\infty }{\mathop{lim }}\frac{x\left( \tfrac{1}{x}+1 \right)}{{{x}^{2}}\left( \tfrac{1}{x}-1 \right)}=0
\underset{x\to -\infty }{\mathop{lim }}\left( \frac{1+x}{1-x}-0\cdot x \right)=-1
I stwierdzam, że asymptoty ukośne istnieją (przy x\to \infty i x\to -\infty , o równaniu y=-1) i poziomych już nie szukam, bo poziome to i tak szczególne ukośne.
W tym konkretnym przykładzie punkt dla podejścia pierwszego, ale jakby były ukośne nie-poziome, drugie podejście jest krótsze.
Mnóstwo przykładów krok-po-kroku na video jest w moim Kursie .
\underset{x\to \infty }{\mathop{lim }}\frac{\frac{1+x}{1-x}}{x}=\underset{x\to \infty }{\mathop{lim }}\frac{1+x}{x-{{x}^{2}}}=\underset{x\to \infty }{\mathop{lim }}\frac{x\left( \tfrac{1}{x}+1 \right)}{{{x}^{2}}\left( \tfrac{1}{x}-1 \right)}=0
Z tego wszystkiego nie rozumiem niestety jednego. Skąd wyszło 0 przy obliczaniu asymptoty ukośnej? Mozna skrócić sobie tak po prostu x i x² i z tego wychodzi nam zero?
No bo to idzie tak:
\underset{x\to \infty }{\mathop{lim }}\frac{\frac{1+x}{1-x}}{x}=\underset{x\to \infty }{\mathop{lim }}\frac{1+x}{x-{{x}^{2}}}=\underset{x\to \infty }{\mathop{lim }}\frac{x\left( \tfrac{1}{x}+1 \right)}{{{x}^{2}}\left( \tfrac{1}{x}-1 \right)}=\underset{x\to \infty }{\mathop{lim }}\frac{\tfrac{1}{x}+1}{x\left( \tfrac{1}{x}-1 \right)}
I teraz wiemy, że stała przez nieskończoność dąży do zera: \left[ \frac{A}{\pm \infty } \right]=0(polecam mój Kurs Granic z omówieniem tych wzorów).
Tak więc licznik dąży do 1, a mianownik do nieskończoności. Zatem całość do zera:
\underset{x\to \infty }{\mathop{lim }}\frac{\tfrac{1}{x}+1}{x\left( \tfrac{1}{x}-1 \right)}=0
Polecam zapoznanie się z pochodnymi i regułą de L’Hospitala. Limes dla f(x)/g(x) = limes dla f’/g’. Więc wyciągając kolejne pochodne pochodnych można dojść w tym wypadku do równania (1+x)/(x-x^2) = 1/(1-2x) = 0/2 = 0 i dlatego współczynnik ‘a’ w równaniu y=ax+b jest równy 0 czyli pochodna jest pozioma. Co za tym idzie oznacza to obecność ekstremum funkcji w przedziale. Naprawdę ułatwiają te pochodne szybkie i sprawne obliczenia asymptot ukośnych dla wielu funkcji, więc serdecznie polecam 😉
heh
A co jeśli podczas liczenia asymptoty skośnej wyjdzie nam nieskończoność?
Wtedy asymptota ukośna nie istnieje (no i oczywiście pozioma też, bo każda pozioma to ukośna), tam gdzie wyszła nam nieskończoność (a mogła nam wyjść przy x->+{\infty} lub x->-{\infty} lub tu i tu).
Super wyjaśnione 🙂