أنظمة المعادلات المتجانسة (عدد الحلول باستخدام رتبة المصفوفة)

---

أنظمة المعادلات الخطية المتجانسة هي تلك الأنظمة التي تكون جميع الحدود الحرة فيها مساوية للصفر. تبدو هذه الأنظمة كما يلي:

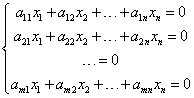
على سبيل المثال:

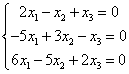
عدد الحلول الممكنة في أنظمة المعادلات الخطية

لنتذكر أنه في كل نظام من المعادلات الخطية هناك ثلاث حالات ممكنة:

1. النظام لديه حل واحد (عندما رتبة المصفوفة الرئيسية = رتبة المصفوفة المكملة = عدد المجاهيل في النظام: )
2. النظام لديه حلول لا نهائية (عندما رتبة المصفوفة الرئيسية = رتبة المصفوفة المكملة وتكون أصغر من عدد المجاهيل في النظام )
3. النظام ليس لديه حلول (عندما رتبة المصفوفة الرئيسية لا تساوي رتبة المصفوفة المكملة)

المصفوفة المكملة هي المصفوفة الرئيسية مع إضافة عمود الحدود الحرة. في حالة النظام المتجانس، سيكون هذا العمود مكوناً من أصفار فقط. أثناء حساب الرتب يمكن ببساطة حذفها والحصول على المصفوفة الرئيسية فقط.

في مثالنا، رتبة المصفوفة الرئيسية تساوي:

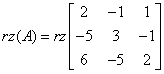
و رتبة المصفوفة المكملة:

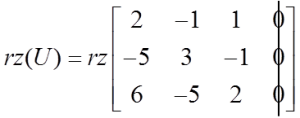
في المثال، يمكننا أن نرى أن ونرى أنه سيكون دائماً كذلك في كل نظام متجانس.

عدد الحلول الممكنة في نظام المعادلات الخطية المتجانسة

إذاً، في نظام المعادلات المتجانسة، ستوجد حالتا الحلول فقط: إما حل واحد أو حلول لا نهائية. سيكون للنظام دائماً حلول، والسؤال الوحيد هو هل سيكون حلاً واحداً أم حلولاً لا نهائية.

دعونا نذهب أبعد من ذلك.

لنعرف ما يسمى “الحل الصفري”. سنسمي الحل الذي تكون فيه قيم جميع المجاهيل تساوي صفرًا حلاً صفريًا.

عند الحديث عن أنظمة المعادلات المتجانسة، يمكن ملاحظة أن:

الحل الصفري هو دائماً حل للنظام المتجانس.

من السهل التحقق من ذلك: إذا وضعنا صفرًا لكل المجهولات في المعادلات، نرى بوضوح أن كل معادلة في النظام المتجانس ستتحقق، دائماً وفي كل نظام متجانس.

إذا علمنا أن النظام المتجانس للمعادلات الخطية لديه حل واحد (ويكون كذلك عندما )، فإننا نعلم أيضاً أن هذا الحل هو بالتأكيد الحل الصفري.

أما إذا علمنا أن النظام المتجانس للمعادلات الخطية لديه حلول لا نهائية (ويكون كذلك عندما )، فإننا نعلم أن النظام لديه الحل الصفري، ولكن إضافة إلى ذلك، بعض الحلول غير الصفرية.

إذا طُلب منا في المسألة: “تحقق مما إذا كان النظام المتجانس يحتوي على حلول غير صفرية”، يكفي إثبات أنه نظام غير محدد، حيث تكون رتبة المصفوفة الرئيسية والمكملة أقل من عدد المجاهيل.

في بعض الأنظمة، يكون ذلك سهلاً جداً، مثل هذا:

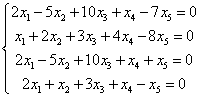
المصفوفة الرئيسية للنظام ستحتوي على 4 صفوف و5 أعمدة، لذا فإن رتبتها ستكون على الأكثر 4. رتبة المصفوفة المكملة ستكون كذلك – ونحن نعلم لماذا. عدد المجاهيل هو 5. وبالتالي يمكن القول على الفور أن النظام غير محدد وأن هناك بعض الحلول غير الصفرية لهذا النظام.